Một cơ sở sản xuất quần áo trẻ em đang bán mỗi bộ quần áo với giá $80$ nghìn đồng một bộ và mỗi tháng cơ sở bán được trung bình $1200$ bộ quần áo

Một cơ sở sản xuất quần áo trẻ em đang bán mỗi bộ quần áo với giá $80$ nghìn đồng một bộ và mỗi tháng cơ sở bán được trung bình $1200$ bộ quần áo. Cơ sở sản suất đang có kế hoạch tăng giá bán để có lợi nhuận tốt hơn. Sau khi tham khảo thị trường, người quản lí thấy rằng nếu từ mức giá $80$ nghìn đồng mà cứ mỗi lần tăng thêm $5$ nghìn đồng mỗi bộ quần áo thì mỗi tháng sẽ bán ít đi $100$ bộ. Biết vốn sản suất một bộ quần áo không thay đổi là $50$ nghìn đồng. Để lợi nhuận thu được lớn nhất thì cơ sở sản xuất đưa ra giá bán cho một bộ quần áo là bao nhiêu? (đơn vị: nghìn đồng).
Đáp án: 95

Lời giải: Gọi $x$ là số lần tăng giá ( $x{>}0,x\in \mathbb{N}$ ). Khi đó
Giá một bộ quần áo là: $80+5x$ (nghìn đồng).
Số bộ quần áo bán được là: $1200-100x$.
Số tiền thu được là: $T\left( x \right)=\left( 80+5x \right)\left( 1200-100x \right)$ (nghìn đồng).
Lãi thu được $L\left( x \right)=T\left( x \right)-\left( 1200-100x \right).50$ $=\left( 1200-100x \right)\left( 30+5x \right)$ (nghìn đồng).
${L}’\left( x \right)=500\left( 6-2x \right)$

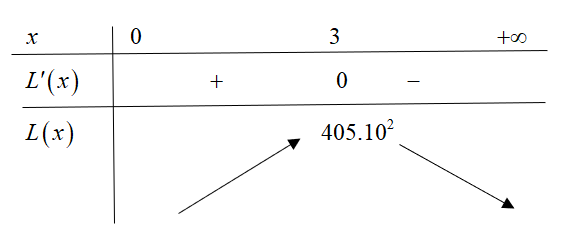
$L\left( x \right)$ lớn nhất khi $x=3$
Vậy giá một bộ quần áo là $95$ nghìn đồng thì lợi nhuận sẽ lớn nhất.