Một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông cạnh $x(cm)$ và chiều cao $h(cm)$

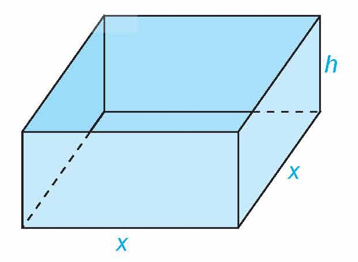
Một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông cạnh $x(cm)$ và chiều cao $h(cm)$. Biết tổng diện tích bề mặt của chiếc hộp bằng $243c{{m}^{2}}$, tìm $x(cm)$ để chiếc hộp có thể tích lớn nhất.

Đáp án: 9

Lời giải: Ta có tổng diện tích bề mặt là: $S={{x}^{2}}+4xh=243\Rightarrow h=\dfrac{243-{{x}^{2}}}{4x}$ với $0{<}x{
Thể tích khối hộp: $V=B.h={{x}^{2}}.h={{x}^{2}}.\dfrac{243-{{x}^{2}}}{4x}=\dfrac{243}{4}x-\dfrac{1}{4}{{x}^{3}}$
Xét hàm số $f(x)=\dfrac{243}{4}x-\dfrac{1}{4}{{x}^{3}}$ trên khoảng $(0;\sqrt{243})$.
Có $f'(x)=\dfrac{243}{4}-\dfrac{3}{4}{{x}^{2}};f'(x)=0\Leftrightarrow \left[ \begin{array}{l} x=9 \\ x=-9 \end{array} \right.$
Có bảng biến thiên:

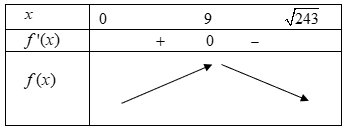
Vậy chiếc hộp có thể tích lớn nhất khi $\text{x}=9(cm)$.