Một chất điểm chuyển động có phương trình chuyển động là $s=-{{t}^{3}}+6{{t}^{2}}+17t$, với $t\left( s \right)$ là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và $s\left( m \right)$ là quãng đường vật đi được trong khoảng thời gian đó

Một chất điểm chuyển động có phương trình chuyển động là $s=-{{t}^{3}}+6{{t}^{2}}+17t$, với $t\left( s \right)$ là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và $s\left( m \right)$ là quãng đường vật đi được trong khoảng thời gian đó. Trong khoảng thời gian 8 giây đầu tiên, vận tốc $v\left( m/s \right)$ của chất điểm đạt giá trị lớn nhất bằng?
Đáp án: 29

Lời giải: Ta có : $v={s}’=-3{{t}^{2}}+12t+17$
Ta đi tìm giá trị lớn nhất của $v=-3{{t}^{2}}+12t+17$ trên khoảng $\left( 0;8 \right)$
Mặt khác: $v’=-6{{t}^{2}}+12$ $=0\Rightarrow t=2$
Bảng biến thiên:

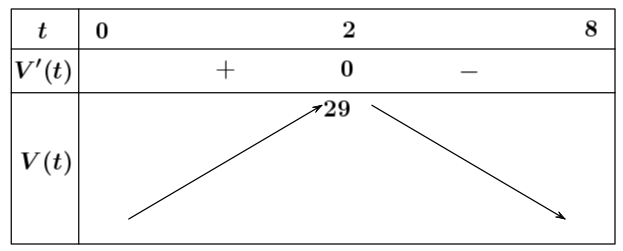
Vậy vận tốc lớn nhất trong khoảng 8 giây đầu tiên là: $29$ (m/s).