Lát cắt ngang của một vùng đất ven biển được mô hình hoá thành một hàm số bậc ba $y=f\left( x \right)$ có đồ thị như hình vẽ (đơn vị độ dài trên các trục là km)

Lát cắt ngang của một vùng đất ven biển được mô hình hoá thành một hàm số bậc ba $y=f\left( x \right)$ có đồ thị như hình vẽ (đơn vị độ dài trên các trục là km).

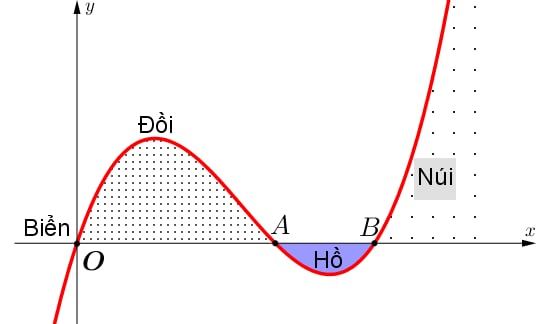
Biết khoảng cách hai bên chân đồi $OA=2\text{km}$, độ rộng của hồ $AB=1\text{km}$ và ngọn đồi cao $528\text{m}$. Tìm độ sâu của hồ (tính bằng mét) tại điểm sâu nhất? (làm tròn đến hàng đơn vị).
Đáp án: 158

Lời giải: Theo đề bài ta có : $OA=2\text{km}$, $OB=3\text{km}$ và $528\text{m=0}\text{,528}\text{km}$.
Đồ thị hàm số $y=f\left( x \right)$ đi qua các điểm $O\left( 0;0 \right)$, $A\left( 2;0 \right),C\left( 3;0 \right)$ suy ra $y=f\left( x \right)=ax\left( x-2 \right)\left( x-3 \right)=a\left( {{x}^{3}}-5{{x}^{2}}+6x \right)$ với $a{>}0$.
Ta có : ${y}’=a\left( 3{{x}^{2}}-10x+6 \right)$, ${y}’=0\Leftrightarrow \left[ \begin{array}{l} x=\dfrac{5+\sqrt{7}}{3} \\ x=\dfrac{5-\sqrt{7}}{3} \end{array} \right.$.
Từ độ cao của đồi ta có tại vị trí điểm cực đại ${{x}_{C}}=\dfrac{5-\sqrt{7}}{3};{{y}_{C}}=0,528$ suy ra $a=\dfrac{0,528}{{{\left( \dfrac{5-\sqrt{7}}{3} \right)}^{3}}-5.{{\left( \dfrac{5-\sqrt{7}}{3} \right)}^{2}}+6.\left( \dfrac{5-\sqrt{7}}{3} \right)}\approx 0,25$.
Điểm sâu nhất của hồ ứng với vị trí của điểm cực tiểu ${{x}_{CT}}=\dfrac{5+\sqrt{7}}{3},{{y}_{CT}}\approx 0,1578$.
Vậy độ sâu của hồ tại điểm sâu nhất xấp xỉ $0,1578\text{km}$ hay xấp xỉ $158\text{m}$.