Hàm số nào dưới đây có bảng biến thiên như sau?

Bài toán gốc

Hàm số nào dưới đây có bảng biến thiên như sau?

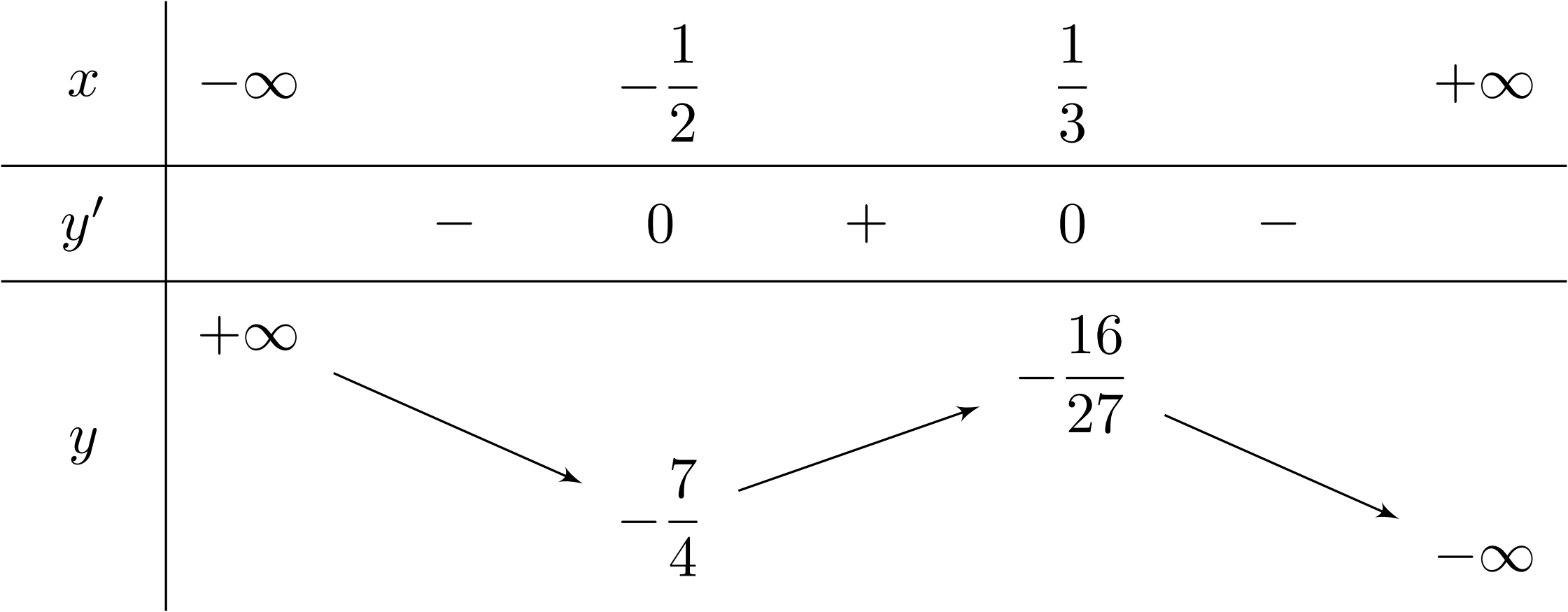
A. $y=-4x^3+x^2+2x-1$.B. $y=-4x^4+x^2-1$.

C. $y=\dfrac{-4x + 4}{x + 4}$.D. $y=-4x^2+x-1$.

Lời giải: Nhìn vào BBT ta thấy đạo hàm $y^{\prime} = 0$ có hai nghiệm $x_1=-\dfrac{1}{2}; x_2=\dfrac{1}{3}$ và hệ số $a = -4{<}0$.
Do đó BBT trên là của đồ thị hàm số $y=-4x^3+x^2+2x-1$.

Phân tích và Phương pháp giải

Dạng bài toán yêu cầu nhận dạng hàm số (bậc ba, bậc bốn trùng phương, hoặc hàm phân thức) thông qua việc phân tích Bảng biến thiên (BBT).

Phương pháp giải bao gồm:

1. Xác định tập xác định và tiệm cận (nếu có) để loại trừ các dạng hàm không phù hợp.

2. Dựa vào giới hạn tại vô cực và chiều biến thiên để xác định bậc của hàm số và dấu của hệ số bậc cao nhất ($a$).

– Nếu $\lim_{x \to \pm\infty} y$ là $\pm\infty$ và có 2 cực trị, đó là hàm bậc ba.

– Nếu $\lim_{x \to \pm\infty} y$ cùng tiến về một giá trị $\pm\infty$ và có 1 hoặc 3 cực trị, đó là hàm trùng phương.

3. Kiểm tra các điểm cực trị (nghiệm của $y’=0$) để khẳng định chính xác hàm số.

Bài toán tương tự

5 bài toán tương tự:

**Câu 1:** Hàm số nào dưới đây có bảng biến thiên mô tả hàm tăng từ $-\infty$ đến điểm cực đại $y(-1)$, sau đó giảm đến điểm cực tiểu $y(1)$, rồi tăng đến $+\infty$? (Hàm số có $D=R$)

A. $y=x^4-2x^2+1$.

B. $y=x^3-3x+1$.

C. $y=\dfrac{x+1}{x-1}$.

D. $y=-x^3+3x$.

Đáp án đúng: B.

Lời giải ngắn gọn: BBT mô tả hàm số bậc ba ($y=ax^3+bx^2+cx+d$) có $a>0$ (lim $y \to +\infty$ khi $x \to +\infty$) và có hai điểm cực trị tại $x=-1$ (CĐ) và $x=1$ (CT). Xét hàm B: $y’=3x^2-3$. $y’=0 \Leftrightarrow x=\pm 1$. Hệ số $a=1>0$. Phù hợp.

**Câu 2:** Cho hàm số $y=f(x)$ có bảng biến thiên mô tả hàm số tăng từ $-\infty$ đến $y(-1)=4$, giảm đến $y(0)=3$, tăng đến $y(1)=4$, và sau đó giảm về $-\infty$. Hỏi đây là hàm số nào?

A. $y=x^3-3x+3$.

B. $y=-x^4+2x^2+3$.

C. $y=\dfrac{-x+3}{x+1}$.

D. $y=x^4-2x^2$.

Đáp án đúng: B.

Lời giải ngắn gọn: BBT mô tả hàm đa thức bậc chẵn (trùng phương) có 3 điểm cực trị ($x=-1, 0, 1$) và $\lim_{x \to \pm\infty} y = -\infty$, suy ra $a<0$. Xét hàm B: $y’=-4x^3+4x = -4x(x^2-1)$. $y’=0 \Leftrightarrow x=0, x=\pm 1$. Hệ số $a=-1<0$. Phù hợp.

**Câu 3:** Bảng biến thiên của hàm số $y=f(x)$ cho thấy hàm số có tiệm cận đứng $x=1$, đồng biến trên $(-\infty; 1)$ và $(1; +\infty)$, và tiệm cận ngang $y=-2$. Hỏi $f(x)$ là hàm nào?

A. $y=\dfrac{-2x+1}{x-1}$.

B. $y=2x^3-x+1$.

C. $y=\dfrac{2x+1}{x-1}$.

D. $y=x^4-4x^2$.

Đáp án đúng: A.

Lời giải ngắn gọn: BBT mô tả hàm phân thức $y=\dfrac{ax+b}{cx+d}$. Tiệm cận đứng $x=-d/c = 1$. Tiệm cận ngang $y=a/c = -2$. Hàm đồng biến, suy ra $y’ > 0$ hay $ad-bc > 0$. Xét hàm A: $y=\dfrac{-2x+1}{x-1}$. $y’ = \dfrac{(-2)(-1) – 1(1)}{(x-1)^2} = \dfrac{1}{(x-1)^2} > 0$. TCĐ $x=1$, TCN $y=-2/1=-2$. Phù hợp.

**Câu 4:** Hàm số nào dưới đây có bảng biến thiên chỉ ra rằng hàm số luôn nghịch biến trên $R$ và $\lim_{x \to -\infty} y = +\infty$, $\lim_{x \to +\infty} y = -\infty$?

A. $y=x^3-x$.

B. $y=-x^3-x+2$.

C. $y=x^4+1$.

D. $y=\dfrac{x+2}{x-1}$.

Đáp án đúng: B.

Lời giải ngắn gọn: BBT mô tả hàm số bậc ba ($a<0$) luôn nghịch biến (không có cực trị). Xét hàm B: $y=-x^3-x+2$. $y’ = -3x^2 – 1$. Vì $y’ < 0$ với mọi $x \in R$. Phù hợp với tính chất luôn nghịch biến và $a=-1 < 0$. **Câu 5:** Bảng biến thiên của hàm số $y=f(x)$ cho thấy hàm số giảm từ $+\infty$ đến cực tiểu $y(0)=-1$, sau đó tăng lên $+\infty$. Hỏi đây là hàm số nào? A. $y=-x^4+3x-1$.
B. $y=x^3-x-1$.

C. $y=x^4-1$.

D. $y=\dfrac{x}{x-1}$.

Đáp án đúng: C.

Lời giải ngắn gọn: BBT mô tả hàm đa thức bậc chẵn ($a>0$) có duy nhất một điểm cực trị (cực tiểu tại $x=0$). Đây là hàm trùng phương $y=ax^4+bx^2+c$ với $a>0$. Xét hàm C: $y=x^4-1$. $y’=4x^3$. $y’=0 \Leftrightarrow x=0$. $y(0)=-1$. Hệ số $a=1>0$. Phù hợp.