Hai thành phố A và B cách nhau một con sông

Hai thành phố A và B cách nhau một con sông. Người ta xây dựng một cây cầu $EF$ bắc qua sông biết rằng thành phố $A$ cách con sông một khoảng là $4km$ và thành phố $B$ cách con sông một khoảng là $6km$ (hình vẽ), biết $HE+KF=20km$ và độ dài $EF$ không đổi. Hỏi xây cây cầu cách thành phố $A$ là bao nhiêu $km$ để đường đi từ thành phố A đến thành phố B là ngắn nhất (đi theo đường $AEFB$ )? (kết quả làm tròn đến phần chục)

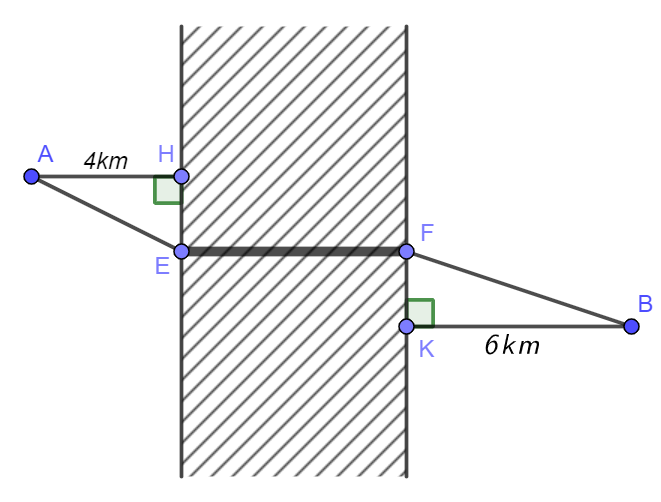
Đáp án: 8,94

Lời giải: Đặt $HE={{x}_{{}}}{{,}_{{}}}FK=y$, với $x,y{>}0$
Ta có: $HE+KF=20\Rightarrow x+y=20$, $\left\{ \begin{array}{l} AE=\sqrt{16+{{x}^{2}}} \\ BF=\sqrt{36+{{y}^{2}}}=\sqrt{36+{{\left( 20-x \right)}^{2}}} \end{array} \right.$
Nhận xét: Vì $EF$ không đổi nên $AB$ ngắn nhất khi $AE+BF$ nhỏ nhất.
Ta có $AE+BF$ $=\sqrt{{{x}^{2}}+16}+\sqrt{{{(20-x)}^{2}}+36}=\sqrt{{{x}^{2}}+16}+\sqrt{{{x}^{2}}-40x+436}=f(x)$
${f}'(x)=\dfrac{x}{\sqrt{{{x}^{2}}+16}}+\dfrac{x-20}{\sqrt{{{x}^{2}}-40x+436}},\forall x\in \left( 0;20 \right)$.
Cho ${f}'(x)=0\Rightarrow x=8$
Bảng biến thiên

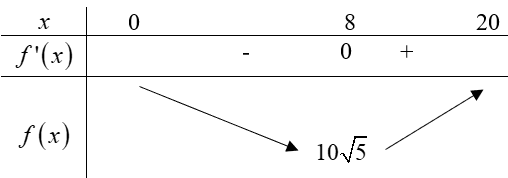
Vậy $AE=\sqrt{{{8}^{2}}+16}\approx 8,94km$