Hai bạn Thành và Linh cùng nhau mở một công ty vận tải taxi điện

Hai bạn Thành và Linh cùng nhau mở một công ty vận tải taxi điện. Hai bạn Thành và Linh dự định sử dụng không quá 10 xe. Nếu công ty sử dụng tối đa thời gian hoạt động của ${x}$ xe điện trên $(1\le x\le 10,x\in \mathbb{N})$ thì doanh thu nhận được của số xe đó là $D(x)={{x}^{3}}-4597{{x}^{2}}+50300x+30000$. Trong khi chi phí nạp điện, bảo dưỡng, phí cầu đường, thuế và thuê nhân công lái xe bình quân cho mỗi xe là $C(x)=3x+300+\dfrac{30000}{x}$. Hai bạn Thành và Linh cần ưu tiên tối đa cho bao nhiêu xe hoạt động thường xuyên để lợi nhuận công ty thu được là lớn nhất?
Đáp án: 5

Lời giải: Chi phí hoạt động cho ${x}$ xe điện là: $x.C(x)=x.\left( 3x+300+\dfrac{30000}{x} \right)=3{{x}^{2}}+300x+30000$.
Lợi nhuận của công ty được tính bằng doanh thu trừ cho chi phí đầu tư.
Suy ra, lợi nhuận của công ty là: $T\left( x \right)=D(x)-x.C\left( x \right)$, $1\le x\le 10$, $x\in \mathbb{N}$.
$T\left( x \right)=\left( {{x}^{3}}-4597{{x}^{2}}+50300x+30000 \right)-\left( 3{{x}^{2}}+300x+30000 \right)$ $={{x}^{3}}-4600{{x}^{2}}+50000x$.
${T}’\left( x \right)=3{{x}^{2}}-9200x+50000$.
${T}’\left( x \right)=0\Leftrightarrow 3{{x}^{2}}-9200x+50000=0\Leftrightarrow \left[ \begin{array}{l} {{x}_{1}}\approx 3061,222218\notin \left[ 1;10 \right] \\ {{x}_{2}}\approx 5,444448485\in \left[ 1;10 \right] \end{array} \right.$
BBT:

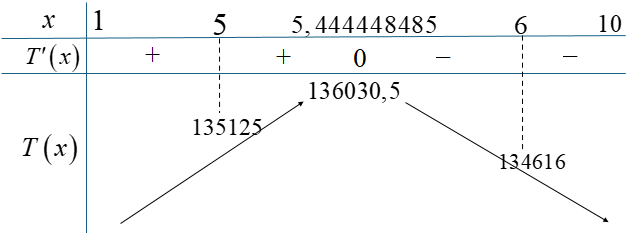
Từ BBT, kết hợp với $x\in \mathbb{N}$ suy ra để lợi nhuận của công ty thu được là lớn nhất thì cần ưu tiên tối đa cho 5 chiếc xe điện hoạt động thường xuyên.