Giả sử chiều cao ( tính bằng $cm$ ) của một giống cây trồng ( trong vòng một số tháng nhất định) tuân theo quy luật logistic được mô hình hoá bằng hàm số $f\left( t \right)=\dfrac{200}{1+4{{e}^{-t}}},\ \ t\ge 0$.
Trong đó thời gian $t$ được tính bằng tháng kể từ khi hạt bắt đầu nảy mầm. Khi đó đạo hàm ${f}’\left( t \right)$ sẽ biểu thị tốc độ tăng chiều cao của giống cây đó. Hỏi sau khi hạt giống bắt đầu nảy mầm thì sau bao nhiêu tháng tốc độ tăng chiều cao của cây là lớn nhất?
Đáp án: 1,38
Lời giải: Ta có: $f\left( t \right)=\dfrac{200}{1+4{{e}^{-t}}}\Rightarrow {f}’\left( t \right)=200.\dfrac{-4.{{e}^{-t}}.\left( -1 \right)}{{{\left( 1+4{{e}^{-t}} \right)}^{2}}}=200.\dfrac{4.{{e}^{-t}}}{{{\left( 1+4{{e}^{-t}} \right)}^{2}}}$
${{f}’}’\left( t \right)=200.\dfrac{-4{{e}^{-t}}{{\left( 1+4{{e}^{-t}} \right)}^{2}}-2\left( 1+4{{e}^{-t}} \right).\left( -4{{e}^{t}} \right).4{{e}^{-t}}}{{{\left( 1+4{{e}^{-t}} \right)}^{4}}}$ $=200.\dfrac{-4{{e}^{-t}}.\left( 1+4{{e}^{-t}} \right)\left( 1+4{{e}^{-t}}-8{{e}^{-t}} \right)}{{{\left( 1+4{{e}^{-t}} \right)}^{4}}}$
$=200.\dfrac{-4{{e}^{-t}}.\left( 1+4{{e}^{-t}} \right)\left( 1-4{{e}^{-t}} \right)}{{{\left( 1+4{{e}^{-t}} \right)}^{4}}}$ $\Rightarrow {{f}’}’\left( t \right)=0\Leftrightarrow {{e}^{-t}}=\dfrac{1}{4}\Leftrightarrow t=-\ln \left( \dfrac{1}{4} \right)=\ln 4\approx 1,38$
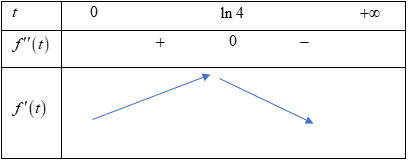
Vậy sau khi nảy mầm khoảng $\ln 4\approx 1,38$ tháng thì cây có tốc độ tăng chiều cao lớn nhất.
