Giả sử chi phí để xuất bản $x$ cuốn tạp chí được cho bởi công thức: $C(x)=0,0001{{x}^{2}}-0,1x+10000$, trong đó $C(x)$ được tính theo đơn vị là vạn đồng

Giả sử chi phí để xuất bản $x$ cuốn tạp chí được cho bởi công thức: $C(x)=0,0001{{x}^{2}}-0,1x+10000$, trong đó $C(x)$ được tính theo đơn vị là vạn đồng. Chi phí phát hành cho mỗi cuốn tạp chí là 3 nghìn đồng. Ta gọi $T(x)$ là tổng chi phí bao gồm chi phí xuất bản và chi phí phát hành cho $x$ cuốn tạp chí. Tỉ số $M(x)=\dfrac{T(x)}{x}$ được gọi là chi phí trung bình cho một cuốn tạp chí khi xuất bản $x$ cuốn. Tìm chi phí trung bình thấp nhất cho một cuốn tạp chí là bao nhiêu vạn đồng, biết rằng nhu cầu hiện tại xuất bản không quá 30000 cuốn?
Đáp án: 2,2

Lời giải: Chi phí phát hành cho mỗi cuốn là 3 nghìn đồng, tức là $0,3$ vạn đồng.
Suy ra chi phí phát hành cho $x$ cuốn là $0,3x$.
Theo đề bài, ta có tổng chi phí xuất bản và phát hành cho $x$ cuốn tạp chí là:
$T\left( x \right)=C\left( x \right)+0,3x=0,0001{{x}^{2}}+0,2x+10000$ với $0{
Xét hàm số $f\left( x \right)=M(x)=\dfrac{T(x)}{x}=0,0001x+0,2+\dfrac{10000}{x}$, với $0{
$\begin{array}{l} {f}’\left( x \right)=0,0001-\dfrac{10000}{{{x}^{2}}}=\dfrac{0,0001{{x}^{2}}-10000}{{{x}^{2}}}; \\ {f}’\left( x \right)=0\Leftrightarrow x=10000\left( \text{do }x{>}0 \right). \\ \lim\limits_{x\to {{0}^{+}}}f(x)=+\infty . \end{array}$
Bảng biến thiên:

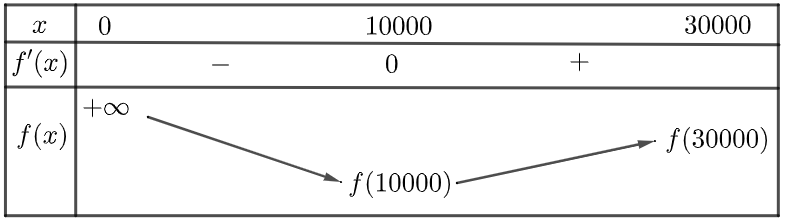
Dựa vào bảng biến thiên, ta thấy giá trị của $M(x)$ nhỏ nhất khi $x=10000$.
Do đó, số lượng tạp chí cần xuất bản sao cho chi phí trung bình thấp nhất là $x=10000$.
Vậy chi phí trung bình cho một cuốn tạp chí khi xuất bản 10000 cuốn là: $M(10000)=2,2$.