Đồ thị dưới đây là của hàm số nào?

Bài toán gốc

Đồ thị dưới đây là của hàm số nào?

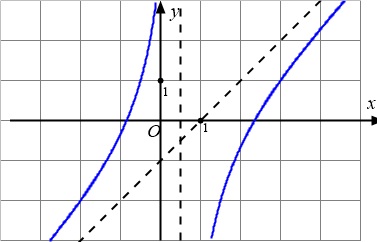
A. $y=\dfrac{2x^2-3x-4}{2x-1}$.B. $y=-2x^3+5x^2+4x+3$.

C. $y=\dfrac{x+5}{-x-2}$.D. $y=\dfrac{x^2+3x+3}{-x-2}$.

Lời giải: Đây là dạng của đồ thị hàm bậc hai chia bậc nhất nên loại các phương án hàm bậc 3 và hàm phân thức bậc nhất chia bậc nhất.
Còn lại hai hàm Phân thức bậc hai chia bậc hai, kiểm tra tiệm cận đứng và tiệm cận xiên để loại trừ, nếu chưa được sẽ lấy điểm thuộc đồ thị thay vào kiểm tra để phân biệt hai hàm số còn lại, nếu chưa được dựa vào số điểm cực trị để phân biệt.

Phân tích và Phương pháp giải

Bài toán yêu cầu nhận dạng hàm số từ đồ thị. Đây là đồ thị hàm phân thức có dạng $y=\dfrac{Ax^2+Bx+C}{ax+b}$ (hàm bậc hai chia bậc nhất), đặc trưng bởi sự tồn tại của Tiệm cận đứng (nghiệm của mẫu) và Tiệm cận xiên (thực hiện phép chia đa thức để tìm thương). Phương pháp giải: 1) Loại trừ các hàm không đúng dạng (bậc 3, bậc nhất/bậc nhất). 2) Kiểm tra Tiệm cận đứng $x = -e/d$. 3) Kiểm tra Tiệm cận xiên $y = mx + k$ bằng phép chia đa thức. 4) Kiểm tra thêm các điểm đặc biệt (cực trị, giao điểm với trục tọa độ) nếu cần.

Bài toán tương tự

1. Đồ thị sau đây là của hàm số nào?

A. $y=\dfrac{x^2-x+1}{x-1}$. B. $y=x^3-3x$. C. $y=\dfrac{x^2-3x+3}{x-2}$. D. $y=\dfrac{x+1}{x-1}$.Đáp án đúng: A. Lời giải ngắn gọn: Đồ thị có Tiệm cận đứng $x=1$ và Tiệm cận xiên $y=x$. Hàm A có VA $x=1$. Phép chia: $(x^2-x+1):(x-1) = x + \dfrac{1}{x-1}$. Tiệm cận xiên $y=x$. Các hàm khác không thỏa mãn.

2. Cho đồ thị hàm số như hình vẽ. Hàm số đó là hàm nào trong các đáp án sau?

A. $y=\dfrac{-x^2+2x+2}{x+1}$. B. $y=\dfrac{x^2-1}{x+1}$. C. $y=\dfrac{-x+2}{x+1}$. D. $y=-x^3+2x^2-x+1$.Đáp án đúng: A. Lời giải ngắn gọn: Đồ thị là dạng bậc hai chia bậc nhất. Tiệm cận đứng $x=-1$. Tiệm cận xiên có hệ số góc âm (khoảng $y=-x+3$). Hàm A: VA $x=-1$. Phép chia: $(-x^2+2x+2):(x+1) = -x+3 – \dfrac{1}{x+1}$. Tiệm cận xiên $y=-x+3$.

3. Đồ thị sau là của hàm số nào?

0′ />

A. $y=\dfrac{2x+3}{x-1}$. B. $y=x^4-2x^2$. C. $y=x^3-3x^2+1$. D. $y=-x^3+x$.Đáp án đúng: C. Lời giải ngắn gọn: Đồ thị có dạng chữ S, là đồ thị hàm bậc ba. Nhánh cuối đi lên ($x \to +\infty, y \to +\infty$) nên hệ số $a$ dương. Chỉ có C là hàm bậc ba với $a=1>0$. Hàm C có hai cực trị tại $x=0$ và $x=2$, khớp với đồ thị.

4. Hàm số nào có đồ thị như hình bên dưới?

A. $y=\dfrac{x^2+1}{2x-4}$. B. $y=\dfrac{x+1}{2-x}$. C. $y=\dfrac{-x-1}{2x-4}$. D. $y=\dfrac{x-1}{2x+1}$.Đáp án đúng: C. Lời giải ngắn gọn: Đây là đồ thị hàm phân thức bậc nhất/bậc nhất ($y=\dfrac{ax+b}{cx+d}$). Đồ thị có Tiệm cận đứng $x=2$ (loại A, D) và Tiệm cận ngang $y=-1/2$. Hàm C: VA $x=2$, HA $y=-1/2$. Kiểm tra giao điểm với Oy: $x=0, y=1/4$. Khớp với đồ thị.

5. Đồ thị trong hình vẽ sau là của hàm số nào?

A. $y=\dfrac{x^2-2x+1}{2x+3}$. B. $y=2x^3+x^2$. C. $y=\dfrac{x^2+2x+1}{x+2}$. D. $y=\dfrac{x+1}{2x+3}$.Đáp án đúng: A. Lời giải ngắn gọn: Đồ thị là hàm bậc hai chia bậc nhất. Tiệm cận đứng $x=-3/2$. Hàm A có VA $x=-3/2$. Tiệm cận xiên: $(x^2-2x+1):(2x+3) = \dfrac{1}{2}x – \dfrac{7}{4} + \dfrac{25/4}{2x+3}$. Tiệm cận xiên $y=\dfrac{1}{2}x – \dfrac{7}{4}$. Đồ thị cho thấy OA có hệ số góc dương, khớp với A.