Đề:    Tìm giá trị lớn nhất, nhỏ nhất của hàm số $y =sin^{20}x + cos^{20}x$

Đề bài:    Tìm giá trị lớn nhất, nhỏ nhất của hàm số $y =sin^{20}x + cos^{20}x$

Lời giải

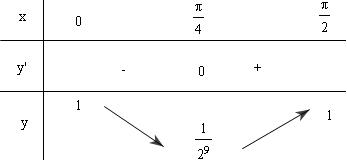
do $sin(x+\frac{\pi}{2} )=cosx$ và $cos(x+\frac{\pi}{2} )=-sinx$ nên $y=sin^{20}x+cos^{20}x$ là hàm tuần hoàn chu kì $\frac{\pi}{2} ,$ do đó cần xét hàm số với $x\in (0,\frac{\pi}{2} )$. Ta có :
$y^/=20sin^{19}x.cosx-20cos^{19}xsinx=20sinxcos^{19}x(tan^{18}x-1)$
$y^/>0\Leftrightarrow  tan^{18}x>1\Leftrightarrow  tanx>1\Leftrightarrow  \frac{\pi}{4} Bảng biến thiên

Do đó $maxy=1$ đạt tại $x=k\frac{\pi}{2} ,miny=\frac{1}{512} $ đạt tại $x=\frac{\pi}{4} +k\frac{\pi}{2} , k\in Z$