Để chặn đường hành lang hình chữ L, người ta dùng một que sào thẳng dài đặt kín những điểm chạm với hành lang (như hình vẽ)

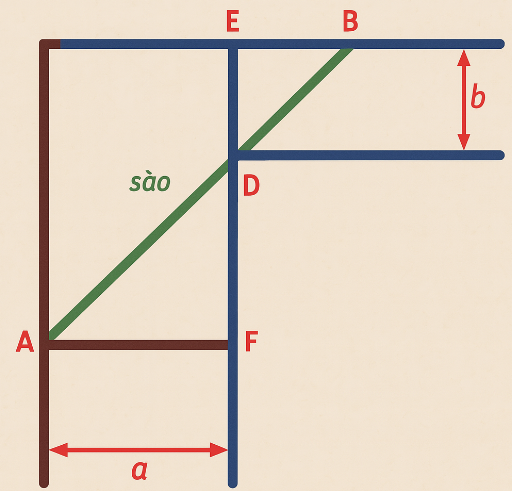
Để chặn đường hành lang hình chữ L, người ta dùng một que sào thẳng dài đặt kín những điểm chạm với hành lang (như hình vẽ). Biết $a=24$ và $b=3$, Biết chiều dài tối thiểu của que sào thỏa mãn điều kiện trên là $l$. Tính giá trị của ${{l}^{2}}$.

Lời giải

Đặt các điểm như hình vẽ.

Đặt $DF=x$, $x>0$, ta có $\Delta ADF$ đồng dạng với $\Delta BED$ nên $\frac{EB}{ED}=\frac{AF}{DF}$$\Rightarrow EB=\frac{ab}{x}$.

Gọi $l$ là chiều dài của que sào, ta có ${{l}^{2}}=A{{B}^{2}}={{\left( x+b \right)}^{2}}+{{\left( a+\frac{ab}{x} \right)}^{2}}=f\left( x \right)$.

${f}’\left( x \right)=2\left( x+b \right)-2\frac{ab}{{{x}^{2}}}\left( a+\frac{ab}{x} \right)=2\left( x+b \right)\left( 1-\frac{{{a}^{2}}b}{{{x}^{3}}} \right)$; ${f}’\left( x \right)=0\Leftrightarrow x=\sqrt[3]{{{a}^{2}}b}=12$.

Xét bảng sau:

Vậy giá trị nhỏ nhất của que sào là $l=\sqrt{1125}$. Giá trị ${{l}^{2}}=1125$.