
Câu hỏi:
Tất cả các giá trị của m để phương trình \({e^x} = m\left( {x + 1} \right)\) có nghiệm duy nhất là:
- A. \(m > 1\)
- B. \(m
- C. \(m
- D. \(m
Hãy chọn trả lời đúng trước khi xem đáp án và lời giải bên dưới.
Có vấn đề về lời giải xin các bạn để lại phản hồi cuối bài.
Có vấn đề về lời giải xin các bạn để lại phản hồi cuối bài.
Đáp án đúng: C
Ta có: \(m = \frac{{{e^x}}}{{x + 1}} = f\left( x \right)\).
Xét hàm số \(f\left( x \right)\)
TXĐ: \(D = \mathbb{R}\backslash {\rm{\{ }} – 1\} .\)
\(f’\left( x \right) = \frac{{x{e^x}}}{{{{\left( {x + 1} \right)}^2}}};\,f’\left( x \right) = 0 \Leftrightarrow x = 0 \Rightarrow f\left( 0 \right) = 1\)
Bảng biến thiên:
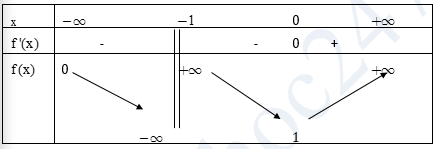
Dựa vào bảng biến thiên ta thấy phương trình có nghiệm duy nhất khim=1 hoặc m
======
Xem lại lý thuyết và ví dụ học toán 12
