Có bao nhiêu số nguyên \(m\) để phương trình \({\log _3}\frac{{2{x^2} + 3x + m}}{{{x^2} – x + 2}} = {x^2} – 6x + 7 – m\) có hai nghiệm phân biệt lớn hơn 1. A.\(4\). B. Vô số. C. \(2\). D. \(3\).

Có bao nhiêu số nguyên \(m\) để phương trình \({\log _3}\frac{{2{x^2} + 3x + m}}{{{x^2} – x + 2}} = {x^2} – 6x + 7 – m\) có hai nghiệm phân biệt lớn hơn 1.
A.\(4\). B. Vô số. C. \(2\). D. \(3\).
Lời giải chi tiết
PHÁT TRIỂN TƯƠNG TỰ CÂU 47 ĐỀ TOÁN THAM KHẢO 2021 CỦA BỘ.
BIÊN SOẠN TỪ STRONG TEAM TOÁN VDC – BIÊN TẬP WEB BOOKTOAN.COM

Điều kiện: \(2{x^2} + 3x + m > 0\).
Ta có:
\({\log _3}\frac{{2{x^2} + 3x + m}}{{{x^2} – x + 2}} = {x^2} – 6x + 7 – m\)\( \Leftrightarrow {\log _3}\left( {\frac{{2{x^2} + 3x + m}}{{{x^2} – x + 2}}} \right) – 1 = {x^2} – 6x + 6 – m\)
\( \Leftrightarrow {\log _3}\frac{{2{x^2} + 3x + m}}{{3{x^2} – 3x + 6}} = 3{x^2} – 3x + 6 – \left( {2{x^2} + 3x + m} \right)\)
\( \Leftrightarrow {\log _3}\left( {2{x^2} + 3x + m} \right) – {\log _3}\left( {3{x^2} – 3x + 6} \right) = \left( {3{x^2} – 3x + 6} \right) – \left( {2{x^2} + 3x + m} \right)\)
\( \Leftrightarrow {\log _3}\left( {2{x^2} + 3x + m} \right) + \left( {2{x^2} + 3x + m} \right) = {\log _3}\left( {3{x^2} – 3x + 6} \right) + \left( {3{x^2} – 3x + 6} \right)\) \(\left( 1 \right)\)
Xét hàm số: \(f\left( t \right) = t + {\log _3}t\) trên \(D = \left( {0; + \infty } \right)\), có \(f’\left( t \right) = 1 + \frac{1}{{t.\ln 3}} > 0\), \(\forall t \in D\),
Do đó hàm số \(f\left( t \right)\) đồng biến trên \(D\)
\( \Rightarrow \left( 1 \right) \Leftrightarrow f\left( {3{x^2} – 3x + 6} \right) = f\left( {2{x^2} + 3x + m} \right)\)
\( \Leftrightarrow 3{x^2} – 3x + 6 = 2{x^2} + 3x + m\)\( \Leftrightarrow {x^2} – 6x = m – 6\) \(\left( 2 \right)\).
– Xét hàm số: \(g\left( x \right) = {x^2} – 6x\) trên \(\mathbb{R}\), có \(g’\left( x \right) = 2x – 6 \Rightarrow g’\left( x \right) = 0 \Leftrightarrow x = 3\).
– Bảng biến thiên:

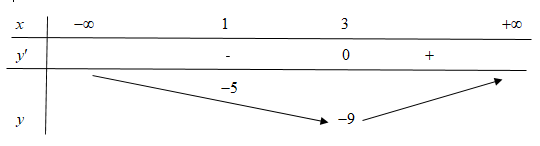
Theo bảng biến thiên ta thấy: phương trình \(\left( 2 \right)\) có hai nghiệm phân biệt lớn hơn \(1\) khi và chỉ khi \( – 9 < m - 6 < - 5\)\( \Leftrightarrow - 3 < m < 1\), do \(m \in \mathbb{Z}\) nên \(m \in \left\{ { - 2; - 1;0} \right\}\), hay có \(3\) giá trị nguyên của \(m\) thỏa mãn yêu cầu bài toán.