Cho một tấm nhôm có dạng hình vuông cạnh ${6 {dm}}$

Cho một tấm nhôm có dạng hình vuông cạnh ${6 {dm}}$. Bác Ánh cắt ở bốn góc bốn hình vuông cùng có độ dài bằng ${x({dm})}$, rồi gập tấm nhôm lại như Hình để được một cái hộp có dạng khối hộp chữ nhật không có nắp. Gọi ${V}$ là thể tích của khối hộp đó tính theo ${x}$.

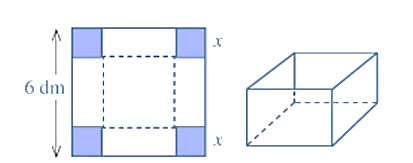
Tìm ${x({dm})}$ để khối hộp tạo thành có thể tích lớn nhất.
Đáp án: 1

Lời giải: Ta thấy độ dài ${x({dm})}$ của cạnh hình vuông bị cắt phải thoả mãn điều kiện ${0{<}x{
Thể tích của khối hộp là ${V(x)=x(6-2 x)^2}$ với ${0{<}x{
Ta phải tìm ${x_0 \in(0 ; 3)}$ sao cho ${V\left(x_0\right)}$ có giá trị lớn nhất.
Ta có: ${V^{\prime}(x)=(6-2 x)^2-4 x(6-2 x)}$
${=(6-2 x)(6-6 x)=12(3-x)(1-x) \text {. } }$
Trên khoảng ${(0 ; 3), V^{\prime}(x)=0}$ khi ${x=1}$.
Bảng biến thiên của hàm số ${V(x)}$ như sau:

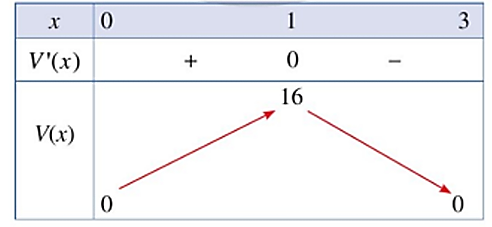
Căn cứ bảng biến thiên, ta thấy: Trên khoảng ${(0 ; 3)}$, hàm số ${V(x)}$ đạt giá trị lớn nhất bằng 16 tại ${x=1}$.
Vậy để khối hộp tạo thành có thể tích lớn nhất thì ${x=1}$ (dm).