Cho hình hộp \(ABCD.A’B’C’D’\)có \(I\)là giao điểm của \(AC\)và \(BD\). Gọi \({V_1}\)và \({V_2}\) lần lượt là thể tích của các khối \(ABCD.A’B’C’D’\) và \(I.A’B’C’\). Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\).

Cho hình hộp \(ABCD.A’B’C’D’\)có \(I\)là giao điểm của \(AC\)và \(BD\). Gọi \({V_1}\)và \({V_2}\) lần lượt là thể tích của các khối \(ABCD.A’B’C’D’\) và \(I.A’B’C’\). Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\).

A. \(\frac{{{V_1}}}{{{V_2}}} = 6\).

B. \(\frac{{{V_1}}}{{{V_2}}} = \frac{3}{2}\).

C. \(\frac{{{V_1}}}{{{V_2}}} = 2\).

D. \(\frac{{{V_1}}}{{{V_2}}} = 3\).

Lời giải:

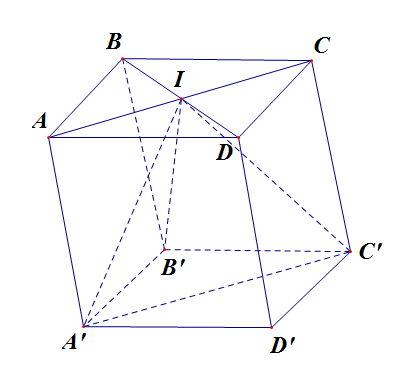
\({V_1} = {V_{ABCD.A’B’C’D’}} = h.{S_{A’B’C’D’}}.\)

\({V_2} = {V_{I.A’B’C’}} = \frac{1}{3}d\left( {I,\left( {A’B’C’} \right)} \right).{S_{A’B’C’}} = \frac{1}{3}h.\frac{1}{2}.{S_{A’B’C’D’}} = \frac{1}{6}h.{S_{A’B’C’D’}}\).

\(\frac{{{V_1}}}{{{V_2}}} = \frac{{h.{S_{A’B’C’D’}}}}{{\frac{1}{6}h.{S_{A’B’C’D’}}}} = 6\).

=========== Đây là các câu ÔN THI TN THPT MÔN TOÁN 2023 – CHUYÊN ĐỀ Trắc nghiệm Thể tích đa diện.