Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(A,\,\,AC = a,\,\,I\) là trung điểm \(SC\). Hình chiếu vuông góc của \(S\) lên \(\left( {ABC} \right)\) là trung điểm \(H\) của \(BC\). Mặt phẳng \(\left( {SAB} \right)\) tạo với \(\left( {ABC} \right)\) một góc \(60^\circ \). Tính khoảng cách từ \(I\) đến mặt phẳng \(\left( {SAB} \right)\).

Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(A,\,\,AC = a,\,\,I\) là trung điểm \(SC\). Hình chiếu vuông góc của \(S\) lên \(\left( {ABC} \right)\) là trung điểm \(H\) của \(BC\). Mặt phẳng \(\left( {SAB} \right)\) tạo với \(\left( {ABC} \right)\) một góc \(60^\circ \). Tính khoảng cách từ \(I\) đến mặt phẳng \(\left( {SAB} \right)\).

A. \(\frac{{\sqrt 3 a}}{5}\).

B. \(\frac{{\sqrt 5 a}}{4}\).

C. \(\frac{{\sqrt 3 a}}{4}\).

D. \(\frac{{\sqrt 2 a}}{3}\).

Lời giải:

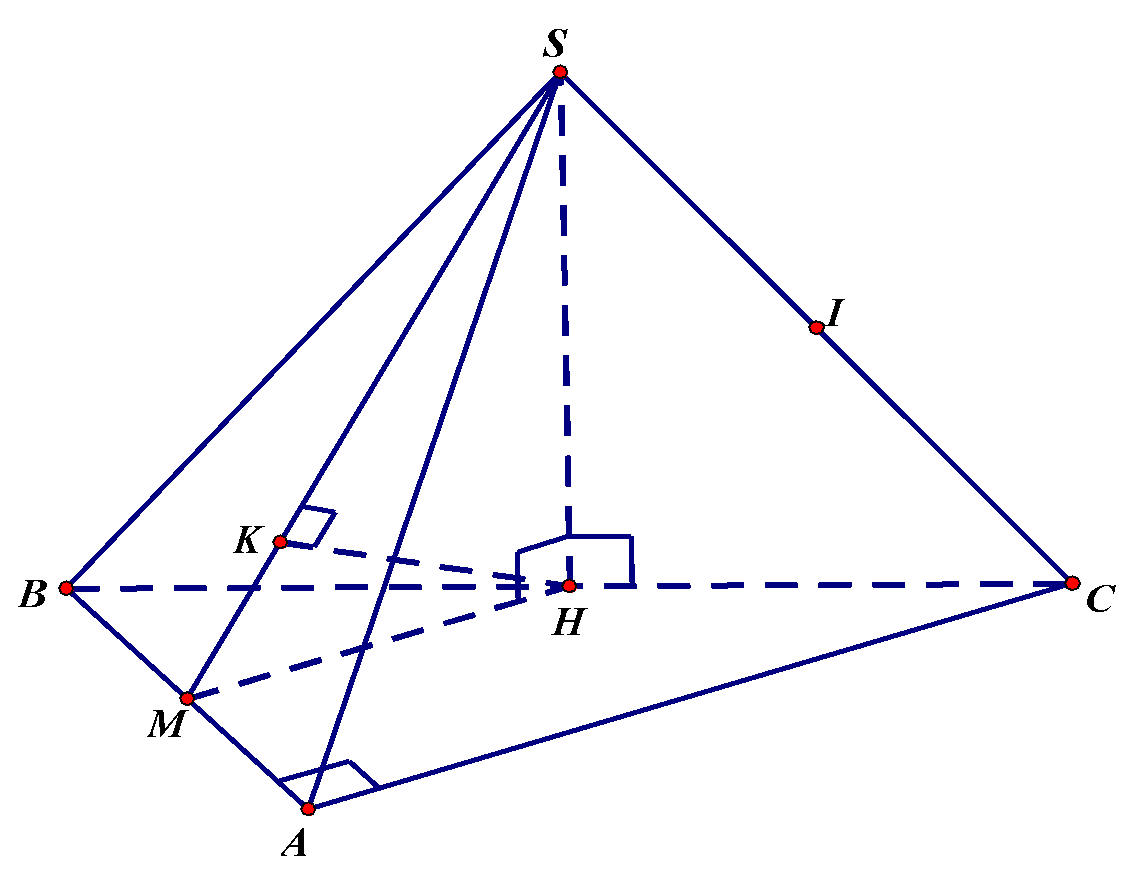
Gọi \(M\) là trung điểm cạnh \(AB\) thì \(MH\) là đường trung bình của tam giác \(ABC\) nên \(MH = \frac{a}{2},\,\,MH{\rm{//AC}}\) \( \Rightarrow MH \bot AB\).

Mặt khác, do \(SH \bot \left( {ABC} \right) \Rightarrow SH \bot AB\) nên \(\left( {SMH} \right) \bot AB \Rightarrow SM \bot AB\). Suy ra góc giữa \(\left( {SAB} \right)\) và \(\left( {ABC} \right)\) là góc giữa \(SM\) và \(MH\); lại có \(SH \bot MH\) nên góc này bằng góc \(\widehat {SMH}\). Từ giả thiết suy ra \(\widehat {SMH} = 60^\circ \).

Gọi \(K\) là hình chiếu của \(H\) lên \(SM\)thì \(HK \bot \left( {SAB} \right)\).

Xét tam giác vuông \(SMH,SH = MH.\tan 60^\circ = \frac{{a\sqrt 3 }}{2},MH = \frac{a}{2} \Rightarrow HK = \frac{{a\sqrt 3 }}{4}\).

Gọi khoảng cách từ \(I,C,H\) đến mặt phẳng \(\left( {SAB} \right)\) lần lượt là \({\rm{d}}\left( {I,\left( {SAB} \right)} \right),{\rm{d}}\left( {C,\left( {SAB} \right)} \right),{\rm{d}}\left( {H,\left( {SAB} \right)} \right)\).

Cách 1: Ta có \(\left\{ \begin{array}{l}{\rm{d}}\left( {I,\left( {SAB} \right)} \right){\rm{ = }}\frac{1}{2}{\rm{d}}\left( {C,\left( {SAB} \right)} \right)\\{\rm{d}}\left( {H,\left( {SAB} \right)} \right) = \frac{1}{2}{\rm{d}}\left( {C,\left( {SAB} \right)} \right)\end{array} \right.\)\( \Rightarrow {\rm{d}}\left( {I,\left( {SAB} \right)} \right) = {\rm{d}}\left( {H,\left( {SAB} \right)} \right) = \frac{{a\sqrt 3 }}{4}\).

Cách 2: \(IH\) là đường trung bình của tam giác \(SBC\) nên \(IH{\rm{//}}SB \Rightarrow IH{\rm{//}}\left( {SAB} \right)\) \( \Rightarrow {\rm{d}}\left( {I,\left( {SAB} \right)} \right) = {\rm{d}}\left( {H,\left( {SAB} \right)} \right) = \frac{{a\sqrt 3 }}{4}.\).

=========== Đây là các câu ÔN THI TN THPT MÔN TOÁN 2023 – CHUYÊN ĐỀ Trắc nghiệm Thể tích đa diện.