Cho hàm số $y=\dfrac{x+1}{{{x}^{2}}+2x+10}$ có giá trị lớn nhất là $M$ và giá trị nhỏ nhất là $m$

Cho hàm số $y=\dfrac{x+1}{{{x}^{2}}+2x+10}$ có giá trị lớn nhất là $M$ và giá trị nhỏ nhất là $m$. Tính giá trị của $36\left( {{M}^{2}}+{{m}^{2}} \right)$.
Đáp án: 2

Lời giải: Ta có $D=\mathbb{R}$.
$y’=\dfrac{-{{x}^{2}}-2x+8}{{{\left( {{x}^{2}}+2x+10 \right)}^{2}}}$.
$y’=0\Leftrightarrow \left[ \begin{array}{l} x=2 \\ x=-4 \end{array} \right.$.
$\lim\limits_{x\to \pm \infty }y=0$.

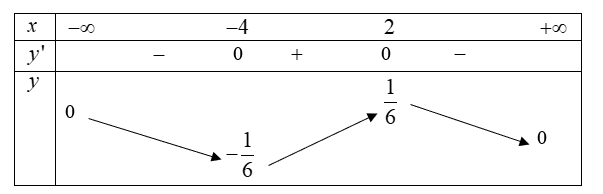
Suy ra $\max\limits_{\mathbb{R}} y=\dfrac{1}{6};\min\limits_{\mathbb{R}} y=-\dfrac{1}{6}$. Vậy $36\left( {{M}^{2}}+{{m}^{2}} \right)=2$.