Cho hàm số $f\left( x \right)=4{{x}^{3}}-9{{x}^{2}}-30x$

Cho hàm số $f\left( x \right)=4{{x}^{3}}-9{{x}^{2}}-30x$. Với các số nguyên $a,b$ mà $a{
Đáp án: -81

Lời giải: Ta có ${f}’\left( x \right)=12{{x}^{2}}-18x-30=0\Leftrightarrow \left[ \begin{array}{l} x=-1 \\ x=\dfrac{5}{2} \end{array} \right.$. Bảng biến thiên

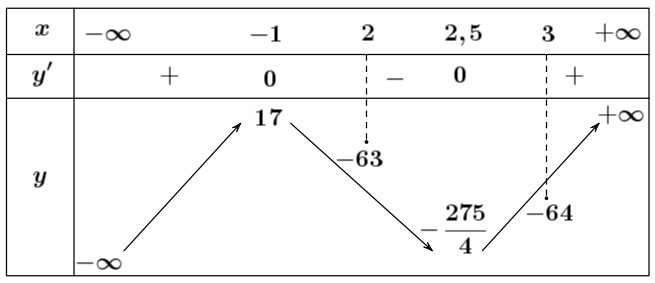
Với các số nguyên $a,b$ mà $a{}0 \end{array} \right.$
$\Rightarrow f\left( b \right)=f\left( 2 \right)=-64;f\left( a \right)=f\left( -1 \right)=17$. Vậy giá trị nhỏ nhất của $f\left( b \right)-f\left( a \right)$ bằng $-81$.