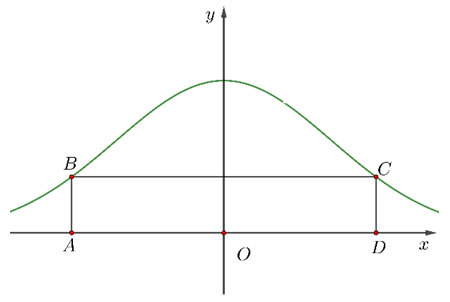
Cho đồ thị hàm số $y=2{{e}^{-{{x}^{2}}}}$ như hình vẽ. $ABCD$ là hình chữ nhật thay đổi sao cho $B$ và $C$ luôn thuộc đồ thị hàm số đã cho và $AD$ nằm trên trục hoành. Diện tích hình chữ nhật $ABCD$ có giá trị lớn nhất bằng bao nhiêu? (làm tròn đến hàng phần trăm)
Đáp án: 1,72
Lời giải: Giả sử điểm $C\left( x;2{{\text{e}}^{-{{x}^{2}}}} \right)$ với $x{>}0$.
Diện tích của hình chữ nhật $ABCD$ là $f\left( x \right)=4x.{{\text{e}}^{-{{x}^{2}}}}$.
Ta có ${f}’\left( x \right)=4{{\text{e}}^{-{{x}^{2}}}}-8{{x}^{2}}{{\text{e}}^{-{{x}^{2}}}}$ $=4{{\text{e}}^{-{{x}^{2}}}}\left( 1-2{{x}^{2}} \right)$.
${f}’\left( x \right)=0$ $\Rightarrow \left[ \begin{array}{l} x=\dfrac{\sqrt{2}}{2}\left( n \right) \\ x=-\dfrac{\sqrt{2}}{2}\left( l \right) \end{array} \right.$.
Bảng biến thiên
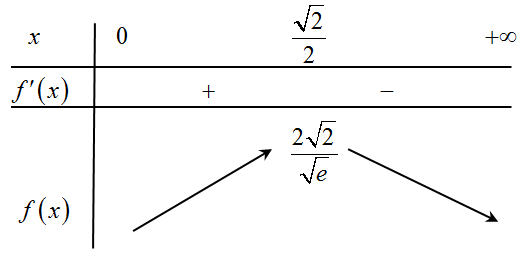
Vậy $\max {{S}_{ABCD}}=\dfrac{2\sqrt{2}}{\sqrt{\text{e}}}$.
Để lại một bình luận