Cho 1 tấm nhôm hình vuông cạnh bằng 10 cm. Người ta cắt ở 4 góc 4 hình vuông có cạnh bằng $x$ cm rồi gập tấm nhôm lại để được 1 cái hộp không nắp. Tìm $x$ để thể tích của cái hộp là lớn nhất? (kết quả làm tròn đến hàng phần chục).
Đáp án: 1,7
Lời giải:
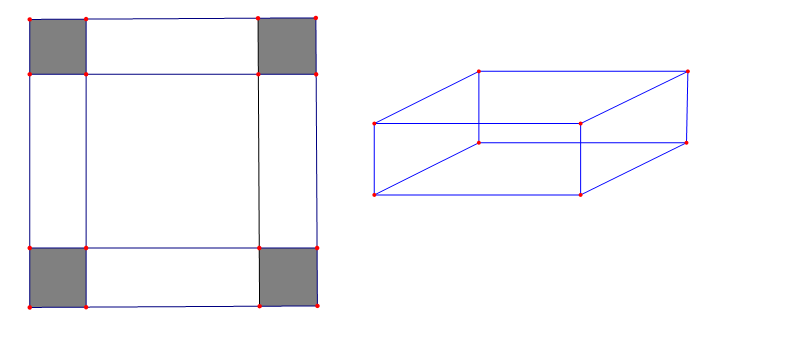
Sau khi gập tấm nhôm lại, ta nhận được một hình hộp chữ nhật có đáy là hình vuông cạnh $10-2x$ và chiều cao bằng $x$ $\left( 0{<}x{
Thể tích hộp là $V=x{{\left( 10-2x \right)}^{2}}=4{{x}^{3}}-40{{x}^{2}}+100x$ với $x\in \left( 0;5 \right)$
${V}’=12{{x}^{2}}-80x+100$
${V}’=0\Leftrightarrow \left[ \begin{array}{l} x=5 \\ x=\dfrac{5}{3} \end{array} \right.$
Bảng biến thiên
ảẢứểđồơđồảđượạựđộ
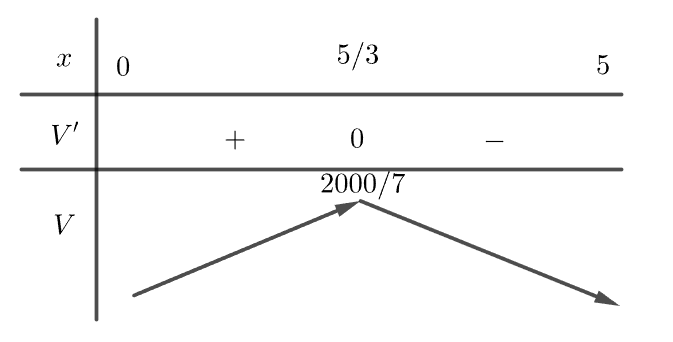
Dựa vào bảng biến thiên thì $x=\dfrac{5}{3}\approx 1,7$ thì thể tích hộp là lớn nhất
Để lại một bình luận