Bạn An có một đoạn dây thép dài $16$ $dm$ muốn uốn thành một kim tự tháp có dạng chóp tứ giác đều (đoạn dây thép được uốn thành 4 cạnh bên và 4 cạnh đáy của kim tự tháp)

Bạn An có một đoạn dây thép dài $16$ $dm$ muốn uốn thành một kim tự tháp có dạng chóp tứ giác đều (đoạn dây thép được uốn thành 4 cạnh bên và 4 cạnh đáy của kim tự tháp). Hỏi thể tích lớn nhất của kim tự tháp bạn An có thể làm được là bao nhiêu? (đơn vị: $d{{m}^{3}}$, kết quả làm tròn đến hàng phần trăm).

Lời giải

Đáp án: 1.95

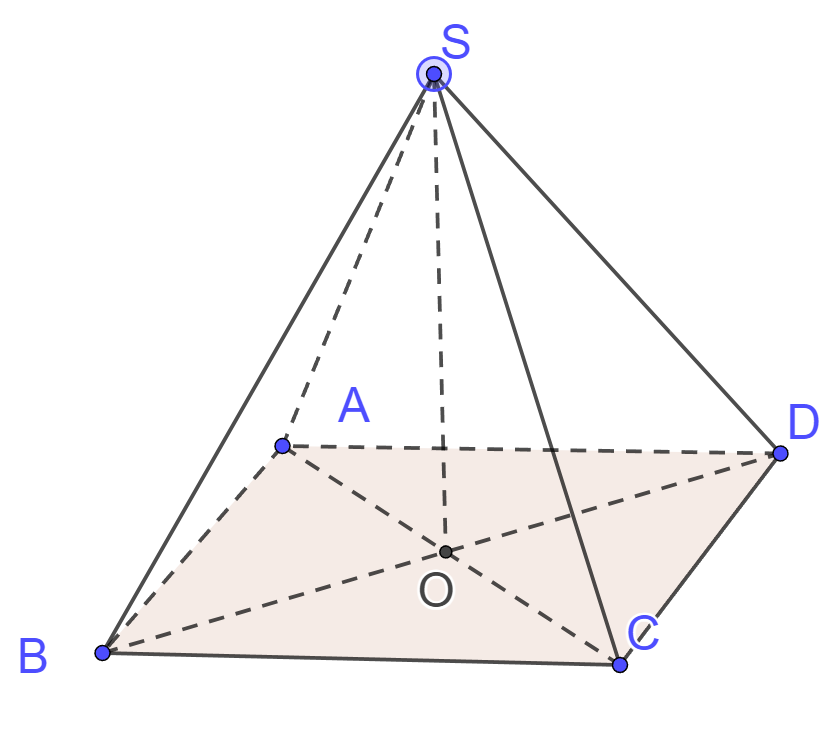
Kí hiệu kim tự tháp dạng chóp tứ giác đều là $S.ABCD$ có đáy tâm $O$ như hình vẽ.

Đặt $AB=x$. Khi đó $SA=4-x\Rightarrow 0<x<4$. Lại có $OC=\frac{x}{\sqrt{2}}$ nên $SO=\sqrt{{{(4-x)}^{2}}-\frac{{{x}^{2}}}{2}}=\sqrt{16-8x+\frac{{{x}^{2}}}{2}}$.

Để $SO$ xác định thì $16-8x+\frac{{{x}^{2}}}{2}>0\Leftrightarrow \left[ \begin{align}

& x<8-4\sqrt{2} \\

& x>8+4\sqrt{2} \\

\end{align} \right.$. Kết hợp với điều kiện $0<x<4$ ta có $0<x<8-4\sqrt{2}$.

Thể tích của chóp là ${{V}_{S.ABCD}}=\frac{1}{3}{{x}^{2}}.\sqrt{16-8x+\frac{{{x}^{2}}}{2}}=\frac{1}{3\sqrt{2}}\sqrt{32{{x}^{4}}-16{{x}^{5}}+{{x}^{6}}}$.

Đặt $f(x)=32{{x}^{4}}-16{{x}^{5}}+{{x}^{6}}$. Ta xét $f(x)$ trên $\left[ 0;8-4\sqrt{2} \right]$.

Ta có: $f'(x)=128{{x}^{3}}-80{{x}^{4}}+6{{x}^{5}}=0\Leftrightarrow \left[ \begin{align}

& x=0 \\

& x=\frac{4(5-\sqrt{13})}{3} \\

& x=\frac{4(5+\sqrt{13})}{3}(L) \\

\end{align} \right.$.

Thay vào ta được $f(0)=f(8-4\sqrt{2})=0$; $f\left( \frac{4(5-\sqrt{13})}{3} \right)\approx 1.95$.

Vậy thể tích lớn nhất của kim tự tháp bạn An có thể làm được là $1,95$.