Câu hỏi: Cho hàm số \(y = f\left( x \right) = {x^3} + a{x^2} + bx + c\) có đồ thị \(\left( C \right)\)đồng thời có 2 điểm cực trị là -1; 1. Biết Parabol\(\left( P \right):y = g(x) = m{x^2} + nx + p\) đi qua hai điểm cực trị của \(\left( C \right)\). Hỏi có bao nhiêu cặp số nguyên dương \(\left( {c;p} \right)\)thỏa mãn \(c + p \le 10\) sao cho hình phẳng giới hạn bởi parabol … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right) = {x^3} + a{x^2} + bx + c\) có đồ thị \(\left( C \right)\)đồng thời có 2 điểm cực trị là -1; 1. Biết Parabol\(\left( P \right):y = g(x) = m{x^2} + nx + p\) đi qua hai điểm cực trị của \(\left( C \right)\). Hỏi có bao nhiêu cặp số nguyên dương \(\left( {c;p} \right)\)thỏa mãn \(c + p \le 10\) sao cho hình phẳng giới hạn bởi parabol \(\left( P \right):y = g(x)\) và đồ thị \(\left( C \right)\) có diện tích bằng 8 ?
Cho parabol \(\left( P \right):y = {x^2}\) và hai điểm \(A\), \(B\) thuộc \(\left( P \right)\) sao cho \(AB = 2\). Tìm giá trị lớn nhất của diện tích hình phẳng giới hạn bởi parabol \(\left( P \right)\) và đường thẳng \(AB\).
Câu hỏi: Cho parabol \(\left( P \right):y = {x^2}\) và hai điểm \(A\), \(B\) thuộc \(\left( P \right)\) sao cho \(AB = 2\). Tìm giá trị lớn nhất của diện tích hình phẳng giới hạn bởi parabol \(\left( P \right)\) và đường thẳng \(AB\). Lời Giải: Đây là các câu trắc nghiệm về ứng dụng tích phân mức độ 3,4 - VẬN DỤNG A. \(\frac{3}{2}\). B. \(\frac{4}{3}\). C. … [Đọc thêm...] vềCho parabol \(\left( P \right):y = {x^2}\) và hai điểm \(A\), \(B\) thuộc \(\left( P \right)\) sao cho \(AB = 2\). Tìm giá trị lớn nhất của diện tích hình phẳng giới hạn bởi parabol \(\left( P \right)\) và đường thẳng \(AB\).
Biết hàm số \(F\left( x \right) = \frac{{{x^5}}}{{20}} – \frac{{{x^4}}}{{12}} – \frac{2}{3}{x^3} + 2{x^2} + 7x\) là nguyên hàm của hàm số \(y = f\left( x \right)\). Gọi \(y = g\left( x \right)\) là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số \(y = f\left( x \right)\). Diện tích hình phẳng giới hạn bởi hai đường \(y = f\left( x \right)\) và \(y = g\left( x \right)\) bằng
Câu hỏi: Biết hàm số \(F\left( x \right) = \frac{{{x^5}}}{{20}} - \frac{{{x^4}}}{{12}} - \frac{2}{3}{x^3} + 2{x^2} + 7x\) là nguyên hàm của hàm số \(y = f\left( x \right)\). Gọi \(y = g\left( x \right)\) là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số \(y = f\left( x \right)\). Diện tích hình phẳng giới hạn bởi hai đường \(y = f\left( x \right)\) và \(y … [Đọc thêm...] vềBiết hàm số \(F\left( x \right) = \frac{{{x^5}}}{{20}} – \frac{{{x^4}}}{{12}} – \frac{2}{3}{x^3} + 2{x^2} + 7x\) là nguyên hàm của hàm số \(y = f\left( x \right)\). Gọi \(y = g\left( x \right)\) là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số \(y = f\left( x \right)\). Diện tích hình phẳng giới hạn bởi hai đường \(y = f\left( x \right)\) và \(y = g\left( x \right)\) bằng
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx – \frac{1}{2}\) và \(g\left( x \right) = d{x^2} + ex + 1\) \(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại 3 điểm có hoành độ lần lượt là \( – 3\); \( – 1\); \(1\) . Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng

Câu hỏi:
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx - \frac{1}{2}\) và \(g\left( x \right) = d{x^2} + ex + 1\) \(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại 3 điểm có hoành độ lần lượt là \( - 3\); \( - 1\); \(1\) . Hình phẳng giới hạn bởi hai đồ thị đã cho có diện … [Đọc thêm...] vềCho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx – \frac{1}{2}\) và \(g\left( x \right) = d{x^2} + ex + 1\) \(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại 3 điểm có hoành độ lần lượt là \( – 3\); \( – 1\); \(1\) . Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
[BT] Đề tham khảo thi TN THPTQG môn Toán năm 2022 – file word có lời giải chi tiết – BT22
[BT] Đề tham khảo thi TN THPTQG môn Toán năm 2022 - file word có lời giải chi tiết - BT22 =========== Đề thi thử của booktoan.com - SỐ 22 có lời giải chi tiết từng câu - file word cho Thầy, Cô biên tập lại cho học sinh thực hành. Bộ đề thi thử THPT QG môn Toán năm 2022 của booktoan.com sưu tầm và biên tập lại. Để có thêm nguồn tư liệu phong phú trong quá trình ôn luyện … [Đọc thêm...] về[BT] Đề tham khảo thi TN THPTQG môn Toán năm 2022 – file word có lời giải chi tiết – BT22
Cho hàm số \(f\left( x \right) = {x^2} – 2|x| + c\) có đồ thị \(\left( C \right)\), gọi hàm số \(y = g\left( x \right)\) là hàm số bậc 2 có đồ thị đi qua 3 điểm cực trị của \(\left( C \right)\), \(S\) là diện tích của hình phẳng giới hạn bởi 2 đường \(f\left( x \right),\,g(x)\). \(S\) thuộc khoảng nào sau đây:
Câu hỏi: Cho hàm số \(f\left( x \right) = {x^2} - 2|x| + c\) có đồ thị \(\left( C \right)\), gọi hàm số \(y = g\left( x \right)\) là hàm số bậc 2 có đồ thị đi qua 3 điểm cực trị của \(\left( C \right)\), \(S\) là diện tích của hình phẳng giới hạn bởi 2 đường \(f\left( x \right),\,g(x)\). \(S\) thuộc khoảng nào sau đây: Lời Giải: Đây là các câu trắc nghiệm về ứng dụng … [Đọc thêm...] vềCho hàm số \(f\left( x \right) = {x^2} – 2|x| + c\) có đồ thị \(\left( C \right)\), gọi hàm số \(y = g\left( x \right)\) là hàm số bậc 2 có đồ thị đi qua 3 điểm cực trị của \(\left( C \right)\), \(S\) là diện tích của hình phẳng giới hạn bởi 2 đường \(f\left( x \right),\,g(x)\). \(S\) thuộc khoảng nào sau đây:
Cho hai hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) và \(y = g\left( x \right) = m{x^2} + nx + k\) cắt nhau tại ba điểm có hoành độ là \( – 1;\frac{1}{2};2\)và có đồ thị như hình vẽ.

Câu hỏi:
Cho hai hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) và \(y = g\left( x \right) = m{x^2} + nx + k\) cắt nhau tại ba điểm có hoành độ là \( - 1;\frac{1}{2};2\)và có đồ thị như hình vẽ.
Biết phần diện tích kẻ sọc bằng \(\frac{{81}}{{32}}\). Diện tích phần hình phẳng giới hạn bởi đồ thị \(y = f\left( x \right),\,y = g\left( x \right)\) và hai đường … [Đọc thêm...] vềCho hai hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) và \(y = g\left( x \right) = m{x^2} + nx + k\) cắt nhau tại ba điểm có hoành độ là \( – 1;\frac{1}{2};2\)và có đồ thị như hình vẽ.
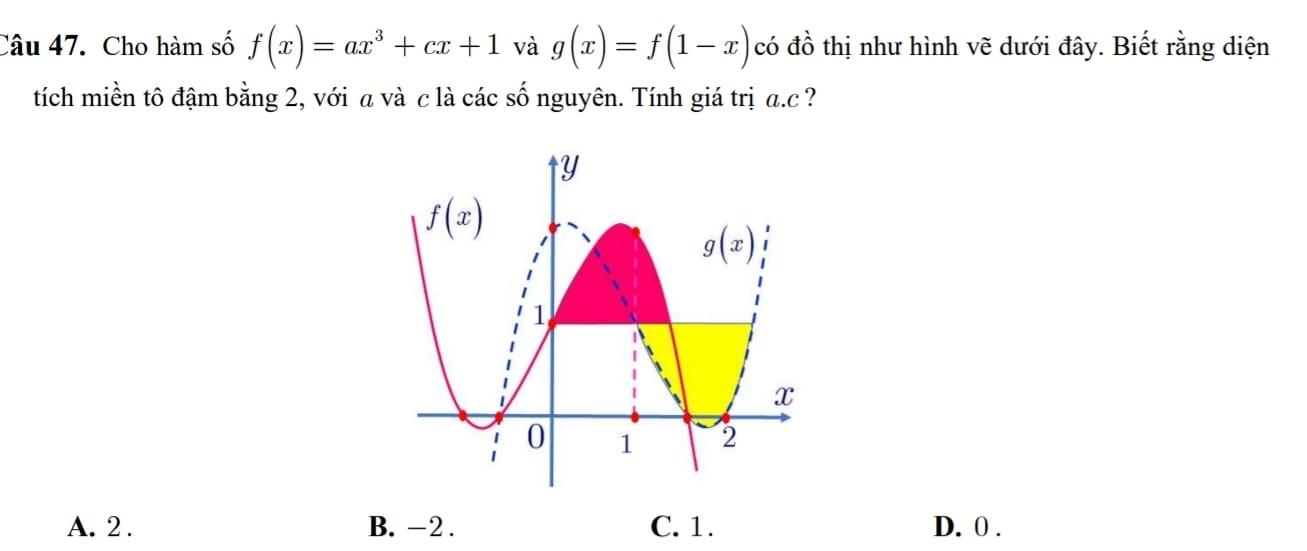
Cho hàm số \(f\left( x \right) = a{x^3} + cx + 1\) và \(g\left( x \right) = f\left( {1 – x} \right)\) có đồ thị như hình vẽ dưới đây. Biết rằng diện tích miền tô đậm bằng 2, với \(a\) và \(c\) là các số nguyên. Tính giá trị \(a.c\)?
Câu hỏi:
Cho hàm số \(f\left( x \right) = a{x^3} + cx + 1\) và \(g\left( x \right) = f\left( {1 - x} \right)\) có đồ thị như hình vẽ dưới đây. Biết rằng diện tích miền tô đậm bằng 2, với \(a\) và \(c\) là các số nguyên. Tính giá trị \(a.c\)?
Lời Giải:
Đây là các câu trắc nghiệm về ứng dụng tích phân mức độ 3,4 - VẬN DỤNG
A. 2.
B. \( - 2\).
C. 1.
D. … [Đọc thêm...] vềCho hàm số \(f\left( x \right) = a{x^3} + cx + 1\) và \(g\left( x \right) = f\left( {1 – x} \right)\) có đồ thị như hình vẽ dưới đây. Biết rằng diện tích miền tô đậm bằng 2, với \(a\) và \(c\) là các số nguyên. Tính giá trị \(a.c\)?
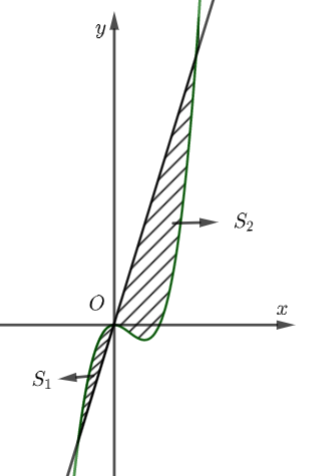
Cho hàm số \(y = 4{x^3} – 3{x^2}\) có đồ thị \(\left( C \right)\) và đường thẳng \(d\) đi qua gốc tọa độ tạo thành hai miền hình phẳng có diện tích \({S_1},{S_2}\) như hình vẽ.
Câu hỏi:
Cho hàm số \(y = 4{x^3} - 3{x^2}\) có đồ thị \(\left( C \right)\) và đường thẳng \(d\) đi qua gốc tọa độ tạo thành hai miền hình phẳng có diện tích \({S_1},{S_2}\) như hình vẽ.
Khi \({S_2} = 12\) thì \({S_1}\) bằng
Lời Giải:
Đây là các câu trắc nghiệm về ứng dụng tích phân mức độ 3,4 - VẬN DỤNG
A. \(\frac{7}{2}\).
B. \(3\).
C. … [Đọc thêm...] vềCho hàm số \(y = 4{x^3} – 3{x^2}\) có đồ thị \(\left( C \right)\) và đường thẳng \(d\) đi qua gốc tọa độ tạo thành hai miền hình phẳng có diện tích \({S_1},{S_2}\) như hình vẽ.
Cho đồ thị \((C)\) của hàm số \(\;y = {x^4} + a{x^3} + d\,\)có một điểm cực tiểu \(\;A\left( { – \frac{3}{2}; – \frac{{107}}{{16}}} \right)\). Gọi \((P)\) là đồ thị hàm số \(g(x)\) có tọa độ đỉnh \(I\left( { – \frac{1}{4};\frac{9}{8}} \right)\) và đi qua điểm \(B\left( { – 1;0} \right)\). Diện tích phần đồ thị giới hạn bởi hai đồ thị hàm số \((C)\), \((P)\) bằng:
Câu hỏi: Cho đồ thị \((C)\) của hàm số \(\;y = {x^4} + a{x^3} + d\,\)có một điểm cực tiểu \(\;A\left( { - \frac{3}{2}; - \frac{{107}}{{16}}} \right)\). Gọi \((P)\) là đồ thị hàm số \(g(x)\) có tọa độ đỉnh \(I\left( { - \frac{1}{4};\frac{9}{8}} \right)\) và đi qua điểm \(B\left( { - 1;0} \right)\). Diện tích phần đồ thị giới hạn bởi hai đồ thị hàm số \((C)\), \((P)\) … [Đọc thêm...] vềCho đồ thị \((C)\) của hàm số \(\;y = {x^4} + a{x^3} + d\,\)có một điểm cực tiểu \(\;A\left( { – \frac{3}{2}; – \frac{{107}}{{16}}} \right)\). Gọi \((P)\) là đồ thị hàm số \(g(x)\) có tọa độ đỉnh \(I\left( { – \frac{1}{4};\frac{9}{8}} \right)\) và đi qua điểm \(B\left( { – 1;0} \right)\). Diện tích phần đồ thị giới hạn bởi hai đồ thị hàm số \((C)\), \((P)\) bằng:
