Câu hỏi:
Một miếng đất dạng hình parabol chiều dài 18m, chiều rộng 12m. Người ta chia miếng đất bằng 2 đoạn thẳng song song \(AB,CD\) thành ba phần có diện tích bằng nhau . Tỉ số \(\frac{{AB}}{{C{\rm{D}}}}\) bằng:
Lời Giải:
Đây là các câu trắc nghiệm về ứng dụng tích phân mức độ 3,4 - VẬN DỤNG
A. \(\frac{1}{{\sqrt[3]{2}}}\).
B. \(\frac{3}{{1 + 2\sqrt 2 … [Đọc thêm...] vềMột miếng đất dạng hình parabol chiều dài 18m, chiều rộng 12m. Người ta chia miếng đất bằng 2 đoạn thẳng song song \(AB,CD\) thành ba phần có diện tích bằng nhau . Tỉ số \(\frac{{AB}}{{C{\rm{D}}}}\) bằng:
Một miếng đất dạng hình parabol chiều dài 18m, chiều rộng 12m. Người ta chia miếng đất bằng 2 đoạn thẳng song song \(AB,CD\) thành ba phần có diện tích bằng nhau . Tỉ số \(\frac{{AB}}{{C{\rm{D}}}}\) bằng:
Cho hàm số \(y = \frac{1}{3}{x^3} – 2{x^2} + 3x – 1\) có đồ thị \(\left( C \right)\). Gọi \(M,N\) là hai điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến tại \(M,N\) song song với nhau. Khi đó diện tích hình phẳng giới hạn bởi \(\left( C \right)\) và đường thẳng \(MN\) nằm trong khoảng nào dưới đây? Biết rằng đường thẳng \(MN\) cắt trục hoành, trục tung lần lượt tại \(A,B\) phân biệt sao cho \(OB = 2OA\).
Câu hỏi: Cho hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x - 1\) có đồ thị \(\left( C \right)\). Gọi \(M,N\) là hai điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến tại \(M,N\) song song với nhau. Khi đó diện tích hình phẳng giới hạn bởi \(\left( C \right)\) và đường thẳng \(MN\) nằm trong khoảng nào dưới đây? Biết rằng đường thẳng \(MN\) cắt trục hoành, trục tung lần lượt … [Đọc thêm...] vềCho hàm số \(y = \frac{1}{3}{x^3} – 2{x^2} + 3x – 1\) có đồ thị \(\left( C \right)\). Gọi \(M,N\) là hai điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến tại \(M,N\) song song với nhau. Khi đó diện tích hình phẳng giới hạn bởi \(\left( C \right)\) và đường thẳng \(MN\) nằm trong khoảng nào dưới đây? Biết rằng đường thẳng \(MN\) cắt trục hoành, trục tung lần lượt tại \(A,B\) phân biệt sao cho \(OB = 2OA\).
Cho hàm số \(f\left( x \right) = {x^3} + b{x^2} + cx + d\). Biết đồ thi hàm số \(f\left( x \right)\) có một điểm cực trị là \(A\) có hoành độ bằng \(1\), đồ thị \(y = f’\left( x \right)\) cắt trục tung tại điểm \(B\) có tung độ là \( – 5\). Gọi \(\Delta \) là đường thẳng đi qua hai điểm \(A\) và \(E\left( { – b – c\,;\,d} \right)\). Tính diện tích hình phẳng giới hạn bởi đường thẳng \(\Delta \) và đồ thi hàm số \(f\left( x \right)\) được tính bởi công thức
Câu hỏi: Cho hàm số \(f\left( x \right) = {x^3} + b{x^2} + cx + d\). Biết đồ thi hàm số \(f\left( x \right)\) có một điểm cực trị là \(A\) có hoành độ bằng \(1\), đồ thị \(y = f'\left( x \right)\) cắt trục tung tại điểm \(B\) có tung độ là \( - 5\). Gọi \(\Delta \) là đường thẳng đi qua hai điểm \(A\) và \(E\left( { - b - c\,;\,d} \right)\). Tính diện tích hình phẳng giới … [Đọc thêm...] vềCho hàm số \(f\left( x \right) = {x^3} + b{x^2} + cx + d\). Biết đồ thi hàm số \(f\left( x \right)\) có một điểm cực trị là \(A\) có hoành độ bằng \(1\), đồ thị \(y = f’\left( x \right)\) cắt trục tung tại điểm \(B\) có tung độ là \( – 5\). Gọi \(\Delta \) là đường thẳng đi qua hai điểm \(A\) và \(E\left( { – b – c\,;\,d} \right)\). Tính diện tích hình phẳng giới hạn bởi đường thẳng \(\Delta \) và đồ thi hàm số \(f\left( x \right)\) được tính bởi công thức
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx – \frac{1}{2}\) và \(g\left( x \right) = d{x^2} + ex + 1\), \(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( – 3\); \( – 1\); \(1\) . Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng

Câu hỏi:
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx - \frac{1}{2}\) và \(g\left( x \right) = d{x^2} + ex + 1\), \(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( - 3\); \( - 1\); \(1\) . Hình phẳng giới hạn bởi hai đồ thị đã cho có … [Đọc thêm...] vềCho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx – \frac{1}{2}\) và \(g\left( x \right) = d{x^2} + ex + 1\), \(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( – 3\); \( – 1\); \(1\) . Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
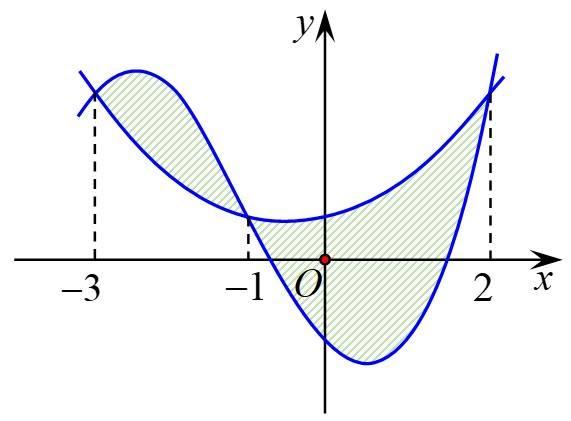
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx – 1\) và \(g\left( x \right) = d{x^2} + ex + \frac{1}{2}\)\(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt \( – 3; – 1;2\) .
Câu hỏi:
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx - 1\) và \(g\left( x \right) = d{x^2} + ex + \frac{1}{2}\)\(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt \( - 3; - 1;2\) .
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích … [Đọc thêm...] vềCho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx – 1\) và \(g\left( x \right) = d{x^2} + ex + \frac{1}{2}\)\(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt \( – 3; – 1;2\) .
Cho hàm số \(y = f(x) = {x^3} + a{x^2} + bx + c\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có hai điểm cực trị là \( – 1\) và \(1\). Gọi \(y = g(x) = m{x^2} + nx + p\,\,\,(m < 0)\) là hàm số bậc hai có cực trị tại \(x = – 1\)và có đồ thị điqua điểm có hoành độ\(x = 1\) của đồ thị hàm số \(y = f\left( x \right)\). Diện tích hình phẳng giới hạnbởi hai đường \(y = f\left( x \right)\) và \(y = g\left( x \right)\) có giá trị nằm trong khoảng nào sau đây?
Câu hỏi: Cho hàm số \(y = f(x) = {x^3} + a{x^2} + bx + c\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có hai điểm cực trị là \( - 1\) và \(1\). Gọi \(y = g(x) = m{x^2} + nx + p\,\,\,(m < 0)\) là hàm số bậc hai có cực trị tại \(x = - 1\)và có đồ thị điqua điểm có hoành độ\(x = 1\) của đồ thị hàm số \(y = f\left( x \right)\). Diện tích hình phẳng giới hạnbởi hai đường \(y = … [Đọc thêm...] vềCho hàm số \(y = f(x) = {x^3} + a{x^2} + bx + c\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có hai điểm cực trị là \( – 1\) và \(1\). Gọi \(y = g(x) = m{x^2} + nx + p\,\,\,(m < 0)\) là hàm số bậc hai có cực trị tại \(x = – 1\)và có đồ thị điqua điểm có hoành độ\(x = 1\) của đồ thị hàm số \(y = f\left( x \right)\). Diện tích hình phẳng giới hạnbởi hai đường \(y = f\left( x \right)\) và \(y = g\left( x \right)\) có giá trị nằm trong khoảng nào sau đây?
Đề VIP dự đoán thi thử TN THPT 2022 – Môn Toán – Đề 10 – File word có lời giải chi tiết
Đề VIP dự đoán thi thử TN THPT 2022 - Môn Toán - Nhóm GV giỏi - Đề 10 - File word có lời giải chi tiết ========= BOOKTOAN.COM GIỚI THIỆU ĐỀ CHO HỌC SINH LUYỆN TẬP KHI LÀM XONG CÓ LỜI GIẢI CHI TIẾT ĐỂ HỌC TẬP. CÓ LỜI GIẢI CHI TIẾT ========== booktoan.com chia sẻ đến các bạn Bộ đề thi thử TN THPT MÔN TOÁN năm 2022. Đề có đáp án chi tiết giúp các bạn đối chiếu, tham khảo để đánh … [Đọc thêm...] vềĐề VIP dự đoán thi thử TN THPT 2022 – Môn Toán – Đề 10 – File word có lời giải chi tiết
Đề VIP dự đoán thi thử TN THPT 2022 – Môn Toán – Đề 9 – File word có lời giải chi tiết
Đề VIP dự đoán thi thử TN THPT 2022 - Môn Toán - Nhóm GV giỏi - Đề 9 - File word có lời giải chi tiết ========= BOOKTOAN.COM GIỚI THIỆU ĐỀ CHO HỌC SINH LUYỆN TẬP KHI LÀM XONG CÓ LỜI GIẢI CHI TIẾT ĐỂ HỌC TẬP. CÓ LỜI GIẢI CHI TIẾT ========== booktoan.com chia sẻ đến các bạn Bộ đề thi thử TN THPT MÔN TOÁN năm 2022. Đề có đáp án chi tiết giúp các bạn đối chiếu, tham khảo để đánh … [Đọc thêm...] vềĐề VIP dự đoán thi thử TN THPT 2022 – Môn Toán – Đề 9 – File word có lời giải chi tiết
Đề VIP dự đoán thi thử TN THPT 2022 – Môn Toán – Đề 8 – File word có lời giải chi tiết
Đề VIP dự đoán thi thử TN THPT 2022 - Môn Toán - Nhóm GV giỏi - Đề 8 - File word có lời giải chi tiết ========= BOOKTOAN.COM GIỚI THIỆU ĐỀ CHO HỌC SINH LUYỆN TẬP KHI LÀM XONG CÓ LỜI GIẢI CHI TIẾT ĐỂ HỌC TẬP. CÓ LỜI GIẢI CHI TIẾT ========== booktoan.com chia sẻ đến các bạn Bộ đề thi thử TN THPT MÔN TOÁN năm 2022. Đề có đáp án chi tiết giúp các bạn đối chiếu, tham khảo để đánh … [Đọc thêm...] vềĐề VIP dự đoán thi thử TN THPT 2022 – Môn Toán – Đề 8 – File word có lời giải chi tiết
Đề VIP dự đoán thi thử TN THPT 2022 – Môn Toán – Đề 7 – File word có lời giải chi tiết
Đề VIP dự đoán thi thử TN THPT 2022 - Môn Toán - Nhóm GV giỏi - Đề 7 - File word có lời giải chi tiết ========= BOOKTOAN.COM GIỚI THIỆU ĐỀ CHO HỌC SINH LUYỆN TẬP KHI LÀM XONG CÓ LỜI GIẢI CHI TIẾT ĐỂ HỌC TẬP. CÓ LỜI GIẢI CHI TIẾT ========== booktoan.com chia sẻ đến các bạn Bộ đề thi thử TN THPT MÔN TOÁN năm 2022. Đề có đáp án chi tiết giúp các bạn đối chiếu, tham khảo để đánh … [Đọc thêm...] vềĐề VIP dự đoán thi thử TN THPT 2022 – Môn Toán – Đề 7 – File word có lời giải chi tiết
