Bài toán gốc Cho hàm số $y=\dfrac{ax+b}{cx+d}$ với $ad-bc \ne 0$ và $c{<}0$ có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?A. $a{<}0, b{<}0, d{<}0$.B. $a{<}0, b{<}0, d{>}0$.C. $a{>}0, b{<}0, d{>}0$.D. $a{>}0, b{>}0, d{<}0$.Lời giải: Theo hàm số và đồ thị ta cóTiệm cận ngang $y=\dfrac{a}{c}$ suy ra $\dfrac{a}{c}{>}0$, vì … [Đọc thêm...] vềCho hàm số $y=\dfrac{ax+b}{cx+d}$ với $ad-bc \ne 0$ và $c{<}0$ có đồ thị như hình vẽ

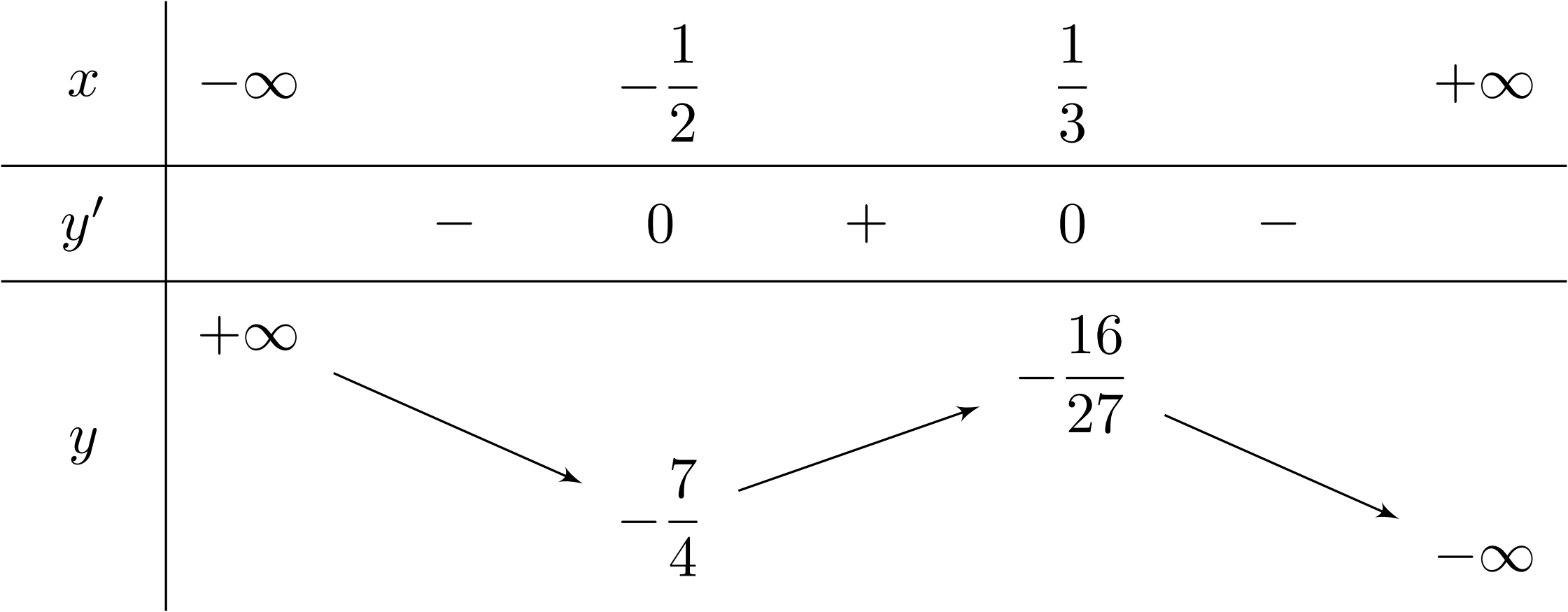
Bài toán gốc Hàm số nào dưới đây có bảng biến thiên như sau?A. $y=-4x^3+x^2+2x-1$.B. $y=-4x^4+x^2-1$.C. $y=\dfrac{-4x + 4}{x + 4}$.D. $y=-4x^2+x-1$.Lời giải: Nhìn vào BBT ta thấy đạo hàm $y^{\prime} = 0$ có hai nghiệm $x_1=-\dfrac{1}{2}; x_2=\dfrac{1}{3}$ và hệ số $a = -4{<}0$.Do đó BBT trên là của đồ thị hàm số $y=-4x^3+x^2+2x-1$. Phân tích và … [Đọc thêm...] vềHàm số nào dưới đây có bảng biến thiên như sau?

Bài toán gốc Tìm $m$ để phương trình $-x^3-3x^2+1=m-1$ có 3 nghiệm?A. $m\in (-2;2)$.B. $m\in (-3;1)$.C. $m\in (-\infty;-3)\cup (1;+\infty)$.D. $m\in (-\infty;-2)\cup (2;+\infty)$.Lời giải: $f(-2)=-3, f(0)=1$ Phân tích và Phương pháp giải Đây là dạng toán tìm điều kiện của tham số $m$ để phương trình đại số (cụ thể là phương trình bậc ba) có số … [Đọc thêm...] vềTìm $m$ để phương trình $-x^3-3x^2+1=m-1$ có 3 nghiệm?

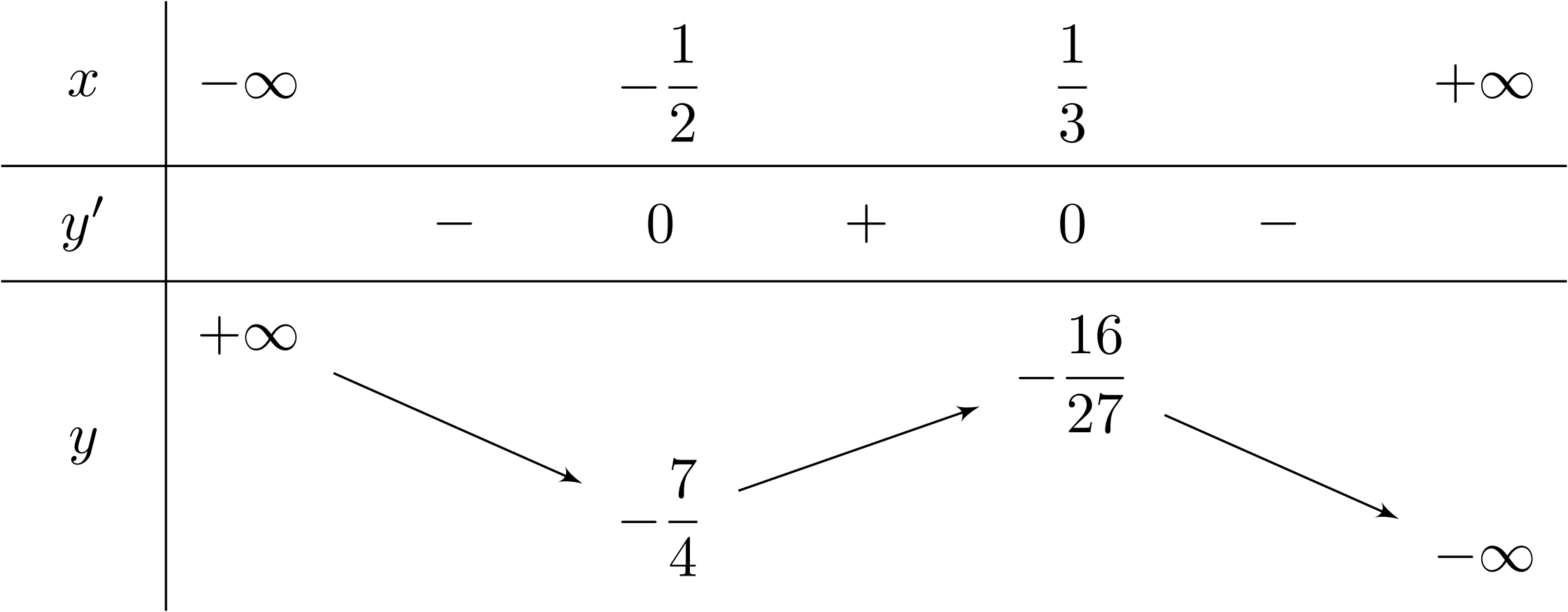
Bài toán gốc Hàm số nào dưới đây có bảng biến thiên như sau?A. $y=\dfrac{-4x + 4}{x + 4}$.B. $y=-4x^3+x^2+2x-1$.C. $y=-4x^2+x-1$.D. $y=-4x^4+x^2-1$.Lời giải: Nhìn vào BBT ta thấy đạo hàm $y^{\prime} = 0$ có hai nghiệm $x_1=-\dfrac{1}{2}; x_2=\dfrac{1}{3}$ và hệ số $a = -4{<}0$.Do đó BBT trên là của đồ thị hàm số $y=-4x^3+x^2+2x-1$.endvabi Phân tích … [Đọc thêm...] vềHàm số nào dưới đây có bảng biến thiên như sau?

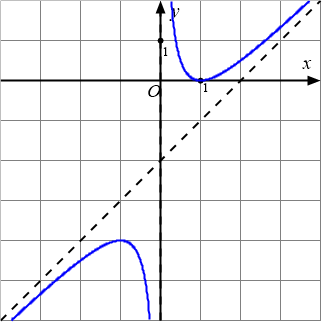
Bài toán gốc Đồ thị dưới đây là của hàm số nào?A. $y=\dfrac{x+2}{x-2}$.B. $y=\dfrac{x^2-2x+1}{x}$.C. $y=-x^3+2x^2+x-3$.D. $y=\dfrac{x^2+2x+2}{-x-1}$.Lời giải: Đây là dạng của đồ thị hàm bậc hai chia bậc nhất nên loại các phương án hàm bậc 3 và hàm phân thức bậc nhất chia bậc nhất.Còn lại hai hàm Phân thức bậc hai chia bậc hai, kiểm tra tiệm cận đứng và tiệm cận xiên để … [Đọc thêm...] vềĐồ thị dưới đây là của hàm số nào?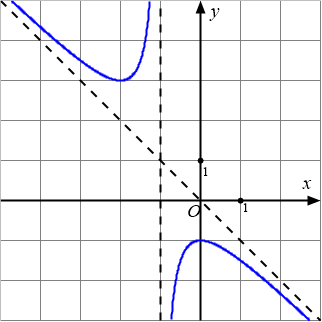

Bài toán gốc Đồ thị dưới đây là của hàm số nào?A. $y=\dfrac{x-3}{-x+2}$.B. $y=x^3-2x^2+2x-5$.C. $y=\dfrac{x^2+x+2}{-x-1}$.D. $y=\dfrac{x^2+x+1}{-x-1}$.Lời giải: Đây là dạng của đồ thị hàm bậc hai chia bậc nhất nên loại các phương án hàm bậc 3 và hàm phân thức bậc nhất chia bậc nhất.Còn lại hai hàm Phân thức bậc hai chia bậc hai có cùng tiệm cận đứng và tiệm cận xiên nên … [Đọc thêm...] vềĐồ thị dưới đây là của hàm số nào?

Bài toán gốc Cho hàm số có đồ thị như hình vẽ bên dưới. Số giao điểm của đồ thị với trục tung làA. $2$.B. $0$.C. $3$.D. $1$.Lời giải: Nhìn vào đồ thị ta thấy đồ thị hàm số cắt trục tung tại một điểm. Phân tích và Phương pháp giải Dạng toán này yêu cầu học sinh nhận biết và đọc các đặc điểm cơ bản của đồ thị hàm số, cụ thể là xác định số lượng … [Đọc thêm...] vềCho hàm số có đồ thị như hình vẽ bên dưới. Số giao điểm của đồ thị với trục tung là

Bài toán gốc Tìm số giao điểm của đồ thị $(C):y=-x^3+10x^2-10x-19$ và $(P):y=2x^2+x+1$.A. 2.B. 1.C. 0.D. 3. Phân tích và Phương pháp giải Dạng bài toán yêu cầu tìm số giao điểm của hai đồ thị hàm số, một là hàm bậc ba ($C$) và một là hàm bậc hai ($P$). Phương pháp giải là lập phương trình hoành độ giao điểm $f(x) = g(x)$. Số nghiệm thực phân … [Đọc thêm...] vềTìm số giao điểm của đồ thị $(C):y=-x^3+10x^2-10x-19$ và $(P):y=2x^2+x+1$.

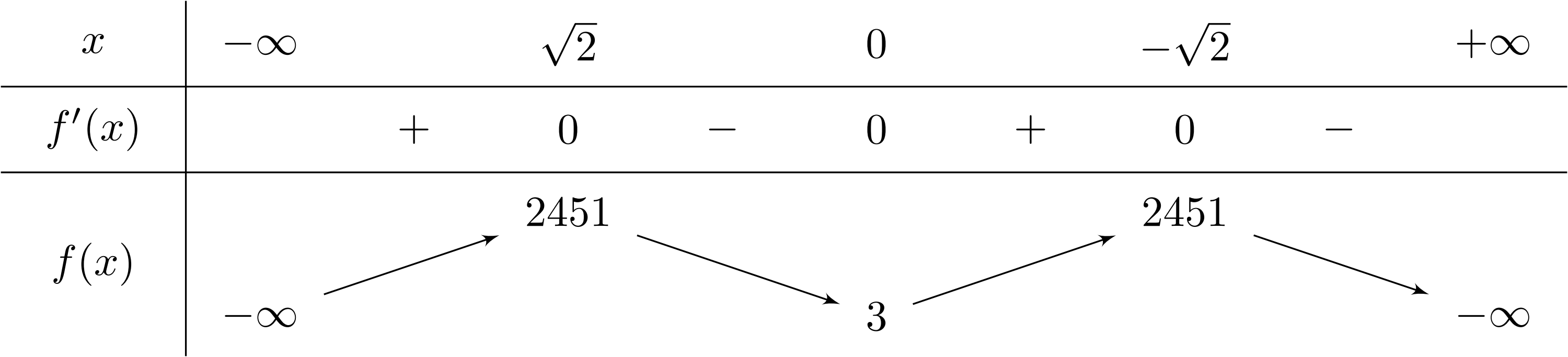
Bài toán gốc Nhìn vào bảng biến thiên dưới đây. Số nghiệm của phương trình $2f(x)+1=0$ làA. $3$.B. $2$.C. $1$.D. $0$.Lời giải: Ta có phương trình $2f(x)+1=0 \Leftrightarrow f(x)=-\dfrac{1}{2}$.Do đó số nghiệm phương trình bằng số giao điểm của đường thẳng $y=-\dfrac{1}{2}$ và đồ thị.Dựa vào đồ thị hàm số trên, ta thấy đường thẳng $y=-\dfrac{1}{2}$ không cắt đồ thị nên … [Đọc thêm...] vềNhìn vào bảng biến thiên dưới đây. Số nghiệm của phương trình $2f(x)+1=0$ là

Bài toán gốc Cho hàm số $y=\dfrac{ax+b}{6x+d}$ có đồ thị như hình vẽ bên. Giá trị biểu thức $T=8a+8b-d$ bằngA. $-692$.B. $-690$.C. $-693$.D. $-689$.Lời giải: Dựa vào hàm số và đồ thị ta cóTiệm cận ngang $y=\dfrac{a}{6}\Rightarrow\dfrac{a}{6}= 5 \Leftrightarrow a=30$.{1 cm}$(1)$Giao trục $Ox$ tại điểm có hoành độ $x_0=\dfrac{-b}{a} \Rightarrow … [Đọc thêm...] vềCho hàm số $y=\dfrac{ax+b}{6x+d}$ có đồ thị như hình vẽ bên. Giá trị biểu thức $T=8a+8b-d$ bằng