Giả sử số lượng của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hoá bằng hàm số $P\left( t \right)=\frac{a}{b+{{\text{e}}^{-0,75t}}}$, trong đó thời gian $t$ được tính bằng giờ. Tại thời điểm ban đầu $t=0$, quần thể có 20 tế bào và tăng với tốc độ 12 tế bào/giờ. Theo mô hình này số lượng nấm men không vượt quá bao nhiêu con?Lời giảiĐáp án: … [Đọc thêm...] vềGiả sử số lượng của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hoá bằng hàm số $P\left( t \right)=\frac{a}{b+{{\text{e}}^{-0,75t}}}$, trong đó thời gian $t$ được tính bằng giờ
Một bể chứa $2{{m}^{3}}$ nước tinh khiết
Một bể chứa $2{{m}^{3}}$ nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ không đổi với tốc độ $20$lít/phút. Nồng độ muối trong bể sau $t$ phút (tính bằng tỉ số của khối lượng muối có trong bể và thể tích nước trong bể, đơn vị gam/lít) là một hàm số $f\left( t \right)$, thời gian tính bằng phút. Biết rằng tiệm cận ngang của đồ thị hàm số $f\left( t \right)$ là … [Đọc thêm...] vềMột bể chứa $2{{m}^{3}}$ nước tinh khiết
Một bể chứa 1000 lít nước muối có nồng độ 0,1 (tính bằng tỉ số của khối lượng muối trong bể và thể tích bể, đơn vị gam/lít)
Một bể chứa 1000 lít nước muối có nồng độ 0,1 (tính bằng tỉ số của khối lượng muối trong bể và thể tích bể, đơn vị gam/lít). Người ta bơm nước muối có nồng độ 0,2 vào bể với tốc độ 20 lít/phút. Gọi $f\left( t \right)$ là nồng độ muối trong bể sau $t$ phút. Tiệm cận ngang của đồ thị hàm số $f\left( t \right)$ là $y=a,\,\left( a\in \mathbb{R} \right)$. Tìm $a$Lời giảiTrả lời : … [Đọc thêm...] vềMột bể chứa 1000 lít nước muối có nồng độ 0,1 (tính bằng tỉ số của khối lượng muối trong bể và thể tích bể, đơn vị gam/lít)
Một tác giả muốn xuất bản một cuốn sách Toán học
Một tác giả muốn xuất bản một cuốn sách Toán học. Biết phí xuất bản là 7 triệu đồng và giá tiền in mỗi cuốn sách là 50 000 đồng. Gọi $t\ \left( t\ge 1 \right)$ là số cuốn sách sẽ in và $f\left( t \right)$ (Đơn vị nghìn đồng) là chi phí trung bình của mỗi cuốn sách. Khi đó, phương trình đường tiệm cận ngang của đồ thị hàm số $f\left( t \right)$ là $y=a,\,\left( a\in \mathbb{R} … [Đọc thêm...] vềMột tác giả muốn xuất bản một cuốn sách Toán học
Một bể chứa $1000$ lít nước tinh khiết
Một bể chứa $1000$ lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ 15 gam muối cho mỗi lít nước với tốc độ 20 lít/phút. Biết rằng nồng độ muối trong bể sau $t$ phút (tính bằng tỉ số của khối lượng muối trong bể và thể tích nước trong bể, đơn vị: gam/lít) là một hàm số $f\left( t \right)$, thời gian $t$ tính bằng phút. Phương trình tiệm cận ngang của đồ thị hàm … [Đọc thêm...] vềMột bể chứa $1000$ lít nước tinh khiết
Một bể chứa $5000$ lít nước tinh khiết
Một bể chứa $5000$ lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ $30$ gam muối cho mỗi lít nước với tốc độ $25$ lít/phút. Nồng độ muối trong bể được tính bởi công thức $f\left( t \right)=\frac{30t}{200+t}$(t là thời gian nước chảy vào bể (phút)). Nồng độ muối lớn nhất mà bể có thể đạt được là bao nhiêu gam/lit? Lời giảiĐáp án: 30Nồng độ muối lớn nhất mà bể có … [Đọc thêm...] vềMột bể chứa $5000$ lít nước tinh khiết
Số lượng sản phẩm bán được của một công ty trong $x$ (tháng) được tính theo công thức$S\left( x \right)=200\left( 5-\frac{9}{2+x} \right)$, trong đó $x\ge 1$
Số lượng sản phẩm bán được của một công ty trong $x$ (tháng) được tính theo công thức$S\left( x \right)=200\left( 5-\frac{9}{2+x} \right)$, trong đó $x\ge 1$.Số lượng sản phẩm lớn nhất mà công ty có thể bán được trong $x$tháng là?Lời giảiĐáp án: 1000Số lượng sản phẩm bán được lớn nhất của công ty là tiệm cận ngang của hàm số $S\left( x \right)$.Tìm tiệm cận ngang của đồ thị hàm … [Đọc thêm...] vềSố lượng sản phẩm bán được của một công ty trong $x$ (tháng) được tính theo công thức $S\left( x \right)=200\left( 5-\frac{9}{2+x} \right)$, trong đó $x\ge 1$
Để loại bỏ $x%$ chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần bỏ ra là $C\left( x \right)=\frac{300x}{100-x}\text{ }$(triệu đồng)$\text{, }0\le x<100$
Để loại bỏ $x%$ chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần bỏ ra là $C\left( x \right)=\frac{300x}{100-x}\text{ }$(triệu đồng)$\text{, }0\le x<100$.Số tiệm cận đứng của đồ thị hàm số $y=C\left( x \right)$ là?Lời giảiĐáp án: 1Tập xác định: $D=\left[ 0;100 \right)$.Xét hàm số $y=C\left( x \right)=\frac{300x}{100-x},0\le x<100$. Ta … [Đọc thêm...] vềĐể loại bỏ $x%$ chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần bỏ ra là $C\left( x \right)=\frac{300x}{100-x}\text{ }$(triệu đồng)$\text{, }0\le x<100$
Cho hàm số $y=ax^3+bx^2+cx+d$ với $a, b, c, d \in \mathbb{R}$ có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?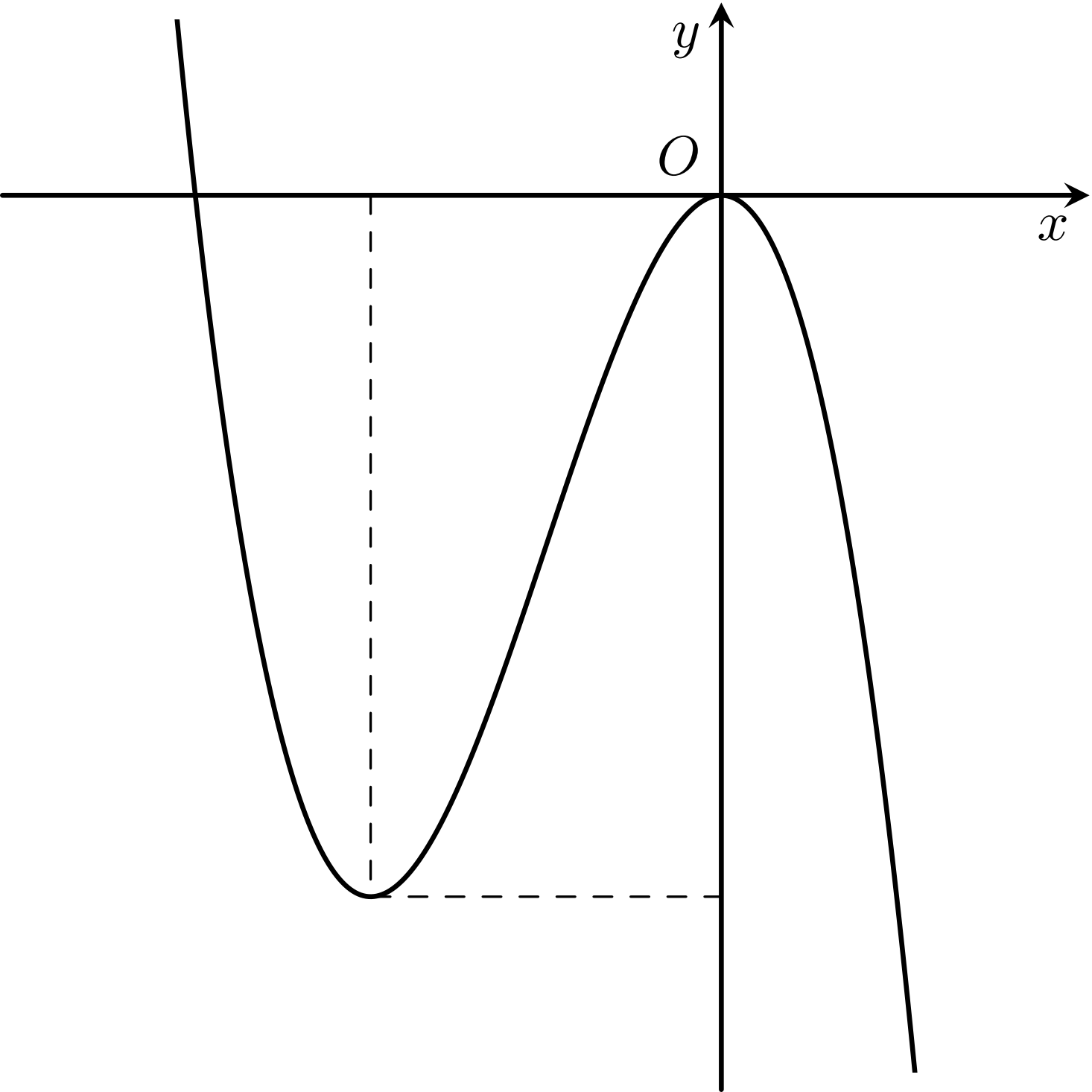

Bài toán gốc Cho hàm số $y=ax^3+bx^2+cx+d$ với $a, b, c, d \in \mathbb{R}$ có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?A. $a{<}0, b{>}0, c=0, d=0$.B. $a{<}0, b=0, c=0, d=0$.C. $a{<}0, b{<}0, c=0, d=0$.D. $a{<}0, b{<}0, c=0, d{>}0$.Lời giải: Từ hình vẽ ta thấyNhánh ngoài cùng bên phải, từ trái sang phải đi xuống nên $a{<}0$.Đồ thị cắt … [Đọc thêm...] vềCho hàm số $y=ax^3+bx^2+cx+d$ với $a, b, c, d \in \mathbb{R}$ có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?

Đồ thị của hàm số nào dưới đây có dạng như đường cong?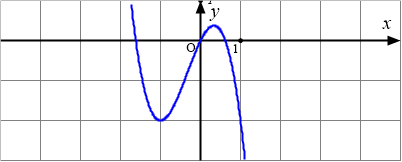

Bài toán gốc Đồ thị của hàm số nào dưới đây có dạng như đường cong?A. $y=\dfrac{-x+5}{5x+3}$.B. $y=-2x^3-2x^2+2x$.C. $y=-3x^4+3x^2-2$.D. $y=-x^2+6x-3$. Phân tích và Phương pháp giải Dạng bài toán là nhận dạng đồ thị hàm số. Phương pháp giải dựa trên việc xác định các đặc điểm cơ bản của đồ thị: 1. Loại hàm số: Xác định đồ thị thuộc loại hàm bậc … [Đọc thêm...] vềĐồ thị của hàm số nào dưới đây có dạng như đường cong?

