Toán học tuổi trẻ – số 498 tháng 12/2018 Mời các bạn xem online và đặt mua báo giấy đọc sẽ tốt hơn ------------- các bạn xem online và tải về: ------------------ -------------- DOWNLOAD HERE -------------- Đón đọc số sau. … [Đọc thêm...] vềToán học tuổi trẻ – số 498 tháng 12/2018
120 bài tập trắc nghiệm tích phân vận dụng cao 2019
120 bài tập trắc nghiệm tích phân vận dụng cao 2019 ----------- các bạn xem online và tải về: ------------------ -------------- DOWNLOAD file PDF … [Đọc thêm...] về120 bài tập trắc nghiệm tích phân vận dụng cao 2019
20 đề ôn tập thi học kỳ 1 Toán 12 – 2018-2019
20 đề ôn tập thi học kỳ 1 Toán 12 - 2018-2019 - có lời giải Các bạn tải về tham khảo. Ôn tập cho HKI năm nay =================== XEM TRỰC TUYẾN ----------------- Đề thi file pdf DOWNLOAD file pdf ---- Đề thi file doc DOWNLOAD file doc … [Đọc thêm...] về20 đề ôn tập thi học kỳ 1 Toán 12 – 2018-2019
Đề thi Học Kỳ 1 Toán lớp 12
Đề thi HK1 Toán lớp 12 tham khảo và các đề thi hk1 các trường trong toàn quốc từ năm 2019 Các đề cập nhật sẽ hiện bên dưới. mời các bạn tham khảo =============== Mục lục: … [Đọc thêm...] vềĐề thi Học Kỳ 1 Toán lớp 12
Đề thi Tham khảo Môn Toán 2019 của bộ giải chi tiết – file word
Đề thi Tham khảo Môn Toán 2019 của bộ giải chi tiết – file word Cấu trúc đề minh họa kỳ thi THPT Quốc gia năm 2019 môn Toán: Chủ đề 1. Ứng dụng đạo hàm để khảo sát sự biến thiên và vẽ đồ thị hàm số. 14 câu Chủ đề 2. Hàm số lũy thừa, hàm số mũ và hàm số logarit. 7 câu Chủ đề 3. Nguyên hàm, tích phân và ứng dụng. 5 câu Chủ đề 4. Số phức. 5 câu Chủ đề 5. … [Đọc thêm...] vềĐề thi Tham khảo Môn Toán 2019 của bộ giải chi tiết – file word
Các công thức tính nhanh Tỷ số thể tích khối đa diện
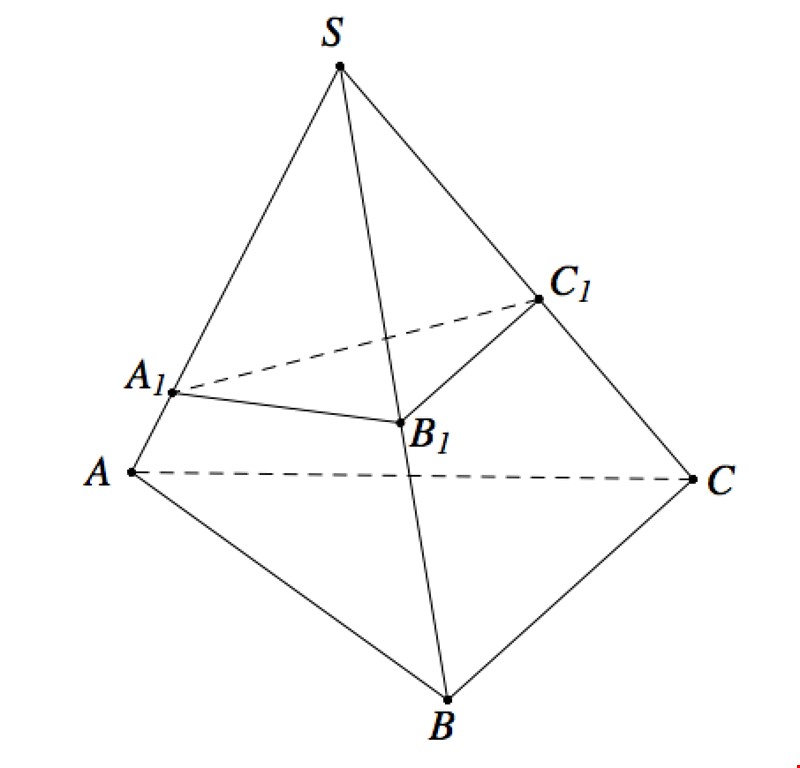
Tổng hợp tất cả các công thức tính nhanh Tỷ số thể tích khối đa diện ----------------- Công thức 1: Hai khối chóp chung đỉnh và chung mặt phẳng đáy $\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{{{S}_{1}}}{{{S}_{2}}}.$ Câu 1. Cho khối chóp $S.ABC$ có thể tích $V.$ Gọi $M,N,P$ lần lượt là trung điểm các cạnh $BC,CA,AB$ và ${V}'$ là thể tích khối chóp $S.MNP.$ Tính tỉ số … [Đọc thêm...] vềCác công thức tính nhanh Tỷ số thể tích khối đa diện
Toán học tuổi trẻ – số 497 tháng 11/2018
Toán học tuổi trẻ – số 497 tháng 11/2018 Mời các bạn xem online và đặt mua báo giấy đọc sẽ tốt hơn ------------- các bạn xem online và tải về: ------------------ -------------- DOWNLOAD HERE -------------- Đón đọc số sau. … [Đọc thêm...] vềToán học tuổi trẻ – số 497 tháng 11/2018
Toán học tuổi trẻ – số 496 tháng 10/2018
Toán học tuổi trẻ – số 496 tháng 10/2018 Mời các bạn xem online và đặt mua báo giấy đọc sẽ tốt hơn ------------- các bạn xem online và tải về: ------------------ -------------- DOWNLOAD HERE -------------- Đón đọc số sau. … [Đọc thêm...] vềToán học tuổi trẻ – số 496 tháng 10/2018
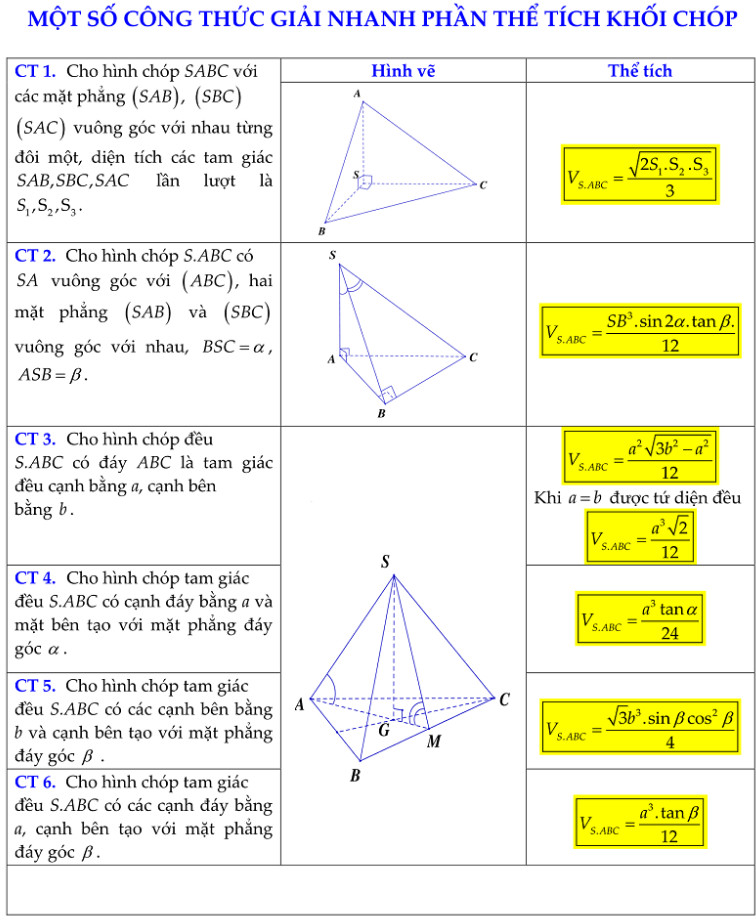
Công thức tính nhanh thể tích khối đa diện
Các công thức tính nhanh này giúp các em có thể làm nhanh các bài toán tính thể tích trong đề thi. Những công thức này có tính ứng dụng rất cao. Mời các bạn xem file ảnh ========== ============== … [Đọc thêm...] vềCông thức tính nhanh thể tích khối đa diện
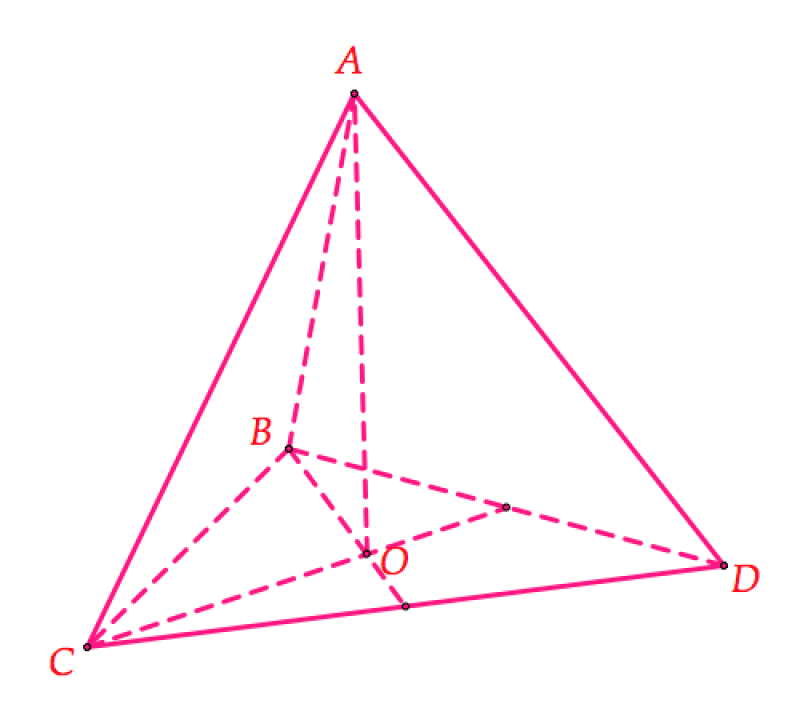
Công thức tính thể tích của 5 khối đa diện đều
Công thức tính thể tích của 5 khối đa diện đều gồm tứ diện đều, khối lập phương, bát diện đều, khối 12 mặt đều và khối 20 mặt đều 1. Tứ diện $ABCD$ đều cạnh $a,$ Ta có $S=\frac{{{a}^{2}}\sqrt{3}}{4}$ và $h=AO=\sqrt{A{{B}^{2}}-O{{B}^{2}}}=\sqrt{{{a}^{2}}-{{\left( \frac{2}{3}.\frac{a\sqrt{3}}{2} \right)}^{2}}}=\frac{a\sqrt{6}}{3}.$ Do đó … [Đọc thêm...] vềCông thức tính thể tích của 5 khối đa diện đều