Đề: Cho tứ diện đều ABCD cạnh bằng x. Mặt cầu tiếp xúc với 6 cạnh tứ diện đều ABCD có bán kính bằng:

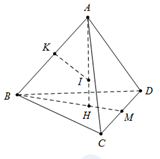
Do tứ diện ABCD đều nên tâm mặt cầu tiếp xúc với 6 cạnh cũng trùng với tâm mặt cầu ngoại tiếp tứ diện.

Gọi H là tâm đường tròn ngoại tiếp tam giác BCD. Suy ra H chính là trọng tâm tam giác BCD.

Khi đó AH chính là trục đường tròn ngoài tiếp tam giác BCD.

Gọi K là trung điểm của AB.

Mặt phẳng trung trực của AB qua K cắt AH tại I chính là tâm mặt cầu ngoại tiếp tứ diện đều ABCD.

Ta có: \(r = IK.\) Mặt khác \(\Delta AKI \sim \Delta AHB \Rightarrow \frac{{AK}}{{AH}} = \frac{{AI}}{{AB}} = \frac{{IK}}{{HB}}.\)

\( \Leftrightarrow \frac{{AB}}{{2{\rm{A}}H}} = \frac{{IK}}{{HB}},\) trong đó \(AB = x,\,\,HB = \frac{{x\sqrt 3 }}{3}.\)

\(AH = \sqrt {A{B^2} – H{B^2}}  = \frac{{x\sqrt 6 }}{3} \Rightarrow r = IK = \frac{{x\sqrt 2 }}{4}.\)