Bác nông dân muốn làm hàng rà trồng ra hình chữ nhật có chiều dài song song với hàng tường gạch

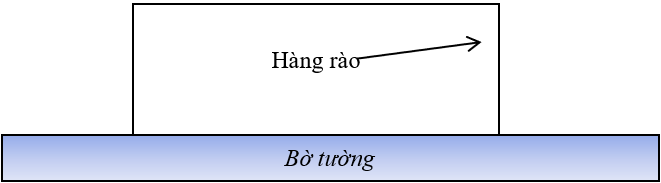
Bác nông dân muốn làm hàng rà trồng ra hình chữ nhật có chiều dài song song với hàng tường gạch. Bác chỉ làm ba mặt hàng rào bởi vì mặt thứ tư bác tận dụng luôn bờ tường. Bác dự tính sẽ dùng 200m lưới để làm nên toàn bộ hàng rào đó. Diện tích đất trồng rau lớn nhất bác có thể rào nên là:

Đáp án: 5000

Lời giải: Trả lời: 5000
Đề Câu cho ta dữ liệu về chu vi của hàng rào là $200m$. Từ đó ta sẽ tìm được mối quan hệ giữa x và r, đến đậy ta có thể đưa về hàm số một biến theo x hoặc theo r như sau:
Ta có:
$x+2r=200\Leftrightarrow r=100-\dfrac{x}{2}$. Từ đây ta có $r{>}0\Rightarrow x$
Diện tích đất rào được tính bởi: $f\left( x \right)=x\left( 100-\dfrac{x}{2} \right)=-\dfrac{{{x}^{2}}}{2}+100x$
Xét hàm số $f\left( x \right)=-\dfrac{{{x}^{2}}}{2}+100x$ trên khoảng $\left( 0;200 \right)$
Đến đây áp dụng quy tắc tìm GTLN của hàm số trên đoạn. ta có:
$f’\left( x \right)=0\Leftrightarrow -x+100=0\Leftrightarrow x=100$
Từ đó ta có $f\left( 100 \right)=5000$ là GTLN của diện tích đất rào được.