Bác Nam dự định làm một máng thoát nước mưa từ một miếng tôn hình chữ nhật có chiều dài $8\left( m \right)$ và chiều rộng $45\left( cm \right)$

Bác Nam dự định làm một máng thoát nước mưa từ một miếng tôn hình chữ nhật có chiều dài $8\left( m \right)$ và chiều rộng $45\left( cm \right)$. Bác Nam chia chiều rộng của miếng tôn thành ba phần bằng nhau, mỗi phần dài $15\left( cm \right)$, rồi gập hai bên lên một góc $\theta$ (đơn vị Radian) như hình vẽ dưới đây.

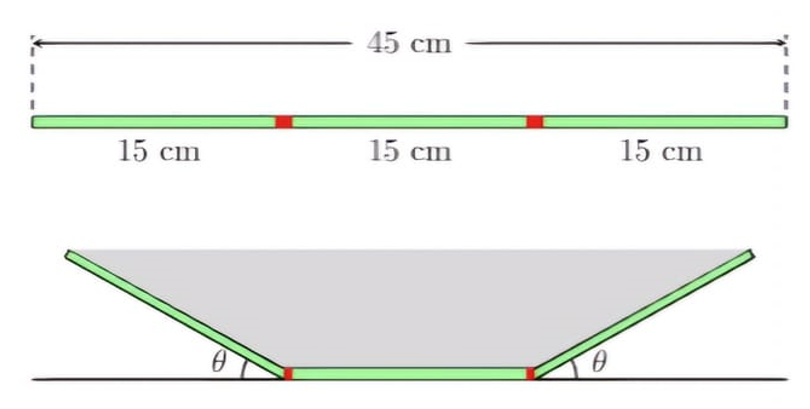
Gọi $S\left( c{{m}^{2}} \right)$ là diện tích của mặt cắt ngang của máng nước. Tìm góc $\theta$ (làm tròn kết quả đến chữ số thập phân thứ hai sau dấu phẩy) để diện tích $S$ là lớn nhất (sẽ cho nước thoát qua máng nhiều nhất).
Đáp án: 1,57

Lời giải: Chiều cao của mặt cắt máng thoát nước là $h=15\sin \left( \theta \right)$.
Từ hình vẽ mặt cắt ta thấy đây là hình thang cân có đáy bé $15\left( cm \right)$, đáy lớn $15+2.15\cos \left( \theta \right)$.
Diện tích mặt cắt ngang được tính bởi công thức:
$S=\dfrac{\left( 30+30\cos \left( \theta \right) \right).15\sin \theta }{2}\left( c{{m}^{2}} \right)$, vớiD9m| $0\le \theta \le \dfrac{\pi }{2}$
$S=225\left( 1+\cos \left( \theta \right) \right).\sin \theta$.
$S=225\left( \sin \left( \theta \right)+\dfrac{1}{2}\sin \left( 2\theta \right) \right)$.
Xét ${S}’\left( \theta \right)=225\left( \cos \theta -\cos \left( 2\theta \right) \right)$
Với ${S}’\left( \theta \right)=0\Leftrightarrow \cos \theta =\cos \left( 2\theta \right)$.
$\Leftrightarrow \left[ \begin{array}{l} \theta =2\theta +k2\pi \\ \theta =-2\theta +k2\pi \end{array} \right.\left( k\in \mathbb{Z} \right)$ $\Leftrightarrow \left[ \begin{array}{l} \theta =-k2\pi \\ \theta =\dfrac{k2\pi }{3} \end{array} \right.\left( k\in \mathbb{Z} \right)$.
Với $\theta =-k2\pi ,0{
Với $\theta =\dfrac{k2\pi }{3},0{
Ta có: ${S}’\left( \theta \right)=0$ vô nghiệm với $0\le \theta \le \dfrac{\pi }{2}$
Với $S\left( \dfrac{\pi }{2} \right)=225$.
Vậy với $\theta =\dfrac{\pi }{2}\approx 1,57$ thì thỏa ycbt.