Anh Tuân muốn xây dựng một hố ga không có nắp đậy dạng hình hộp chữ nhật có thể tích chứ được 3200cm3, tỉ số giữa chiều cao và chiều rộng của hố ga bằng 2

Anh Tuân muốn xây dựng một hố ga không có nắp đậy dạng hình hộp chữ nhật có thể tích chứ được 3200cm3, tỉ số giữa chiều cao và chiều rộng của hố ga bằng 2. Xác định diện tích đáy của hố ga để khi xây hố tiết kiệm được nguyên liệu nhất.
Đáp án: 160

Lời giải: Trả lời: $160$
Gọi $x,y,h$ lần lượt là chiều rộng, chiều dài, chiều cao của hố ga, $\left( x{>}0,y{>}0,h{>}0,cm \right)$
Ta có: $\dfrac{h}{x}=2\Leftrightarrow h=2x$
Thể tích hố ga: $V=xyh\Leftrightarrow y=\dfrac{V}{xh}=\dfrac{1600}{{{x}^{2}}}$
Diện tích cần xây dựng hố ga là:
$\begin{array}{l} S\left( x \right)=xy+2xh+2yh=x.\dfrac{1600}{{{x}^{2}}}+2x2x+x\dfrac{1600}{{{x}^{2}}}2x \\ =\dfrac{1600}{x}+4{{x}^{2}}+\dfrac{6400}{x}=4{{x}^{2}}+\dfrac{8000}{x} \end{array}$
Câu toán trở thành tìm x để S(x) nhỏ nhất.
$\begin{array}{l} S'(x)=8x-\dfrac{8000}{{{x}^{2}}} \\ S'(x)=0\Leftrightarrow 8x-\dfrac{8000}{{{x}^{2}}}=0\Leftrightarrow x=10 \end{array}$
BBT

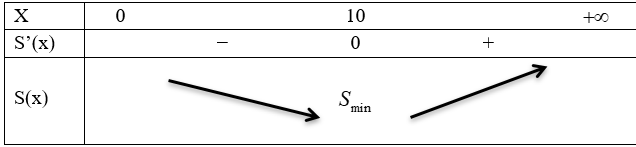
Vậy chiều rộng của hố ga là 10cm, chiều dài là 16cm.
Vậy diện tích đáy hố ga nhỏ nhất là: $S=10.16=160c{{m}^{2}}$.