Anh An muốn thiết kế một bể chứa nước có dạng hình hộp chữ nhật không có nắp, có đáy là hình chữ nhật với chiều dài gấp đôi chiều rộng và diện tích tất cả các mặt của bể nước bằng $150$ m2

Anh An muốn thiết kế một bể chứa nước có dạng hình hộp chữ nhật không có nắp, có đáy là hình chữ nhật với chiều dài gấp đôi chiều rộng và diện tích tất cả các mặt của bể nước bằng $150$ m2. Để thể tích của bể nước là lớn nhất thì chiều dài, chiều rộng và chiều cao của bể nước theo đơn vị mét lần lượt có giá trị là $a,b,c$ mét. Tính giá trị $a+2b+3c$.
Đáp án: 30

Lời giải:

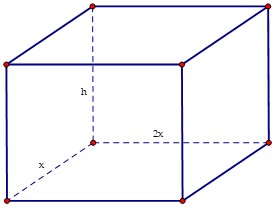
Gọi $x,2x,h$ lần lượt là chiều rộng, dài, cao của bể chứa nước.
Ta có $2{{x}^{2}}+2\left( xh+2xh \right)=150$ $\Leftrightarrow h=\dfrac{150-2{{x}^{2}}}{6x}$ (Điều kiện $0{<}x{
Thể tích bể cá $V=2{{x}^{2}}.\dfrac{150-2{{x}^{2}}}{6x}=\dfrac{1}{3}(150x-2{{x}^{3}})$.
${{V}^{/}}=\dfrac{1}{3}(150-6{{x}^{2}})$. ${{V}^{/}}=0\Rightarrow x=5$.
Lập BBT ta có :

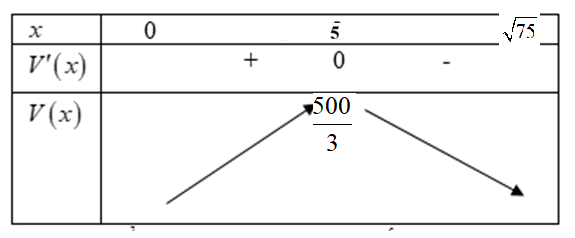
${{V}_{\max }}=\dfrac{500}{3}\Leftrightarrow x=5$. Vậy khi đó $a=10;b=5;c=\dfrac{10}{3}\Rightarrow a+2b+3c=30$