Bài toán gốc
Cho hình lập phương ${ABCD}.{MNPQ}$. Biết góc giữa $\overrightarrow{NQ}$ và $\overrightarrow{BC}$ bằng $a^{\circ}$. Tính $a$? 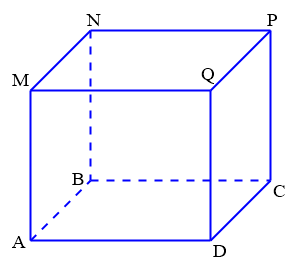
A. $120$ B. $45$ C. $60$ D. $135$
Phân tích và Phương pháp giải
Dạng bài toán yêu cầu xác định góc giữa hai vector trong hình lập phương. Phương pháp giải chủ yếu là sử dụng phép tịnh tiến vector (chuyển vector) để đưa hai vector về cùng một điểm gốc, từ đó góc giữa hai vector được quy về góc trong một tam giác hoặc góc giữa các đường thẳng trong các mặt phẳng cơ bản của hình lập phương. Trong bài toán gốc, ta tịnh tiến $\overrightarrow{BC}$ thành $\overrightarrow{MQ}$. Góc cần tìm là góc giữa $\overrightarrow{NQ}$ và $\overrightarrow{MQ}$, chính là góc $\angle NQM$ trong hình vuông $MNPQ$. Do $MNPQ$ là hình vuông nên $\angle NQM = 45^{\circ}$.
Bài toán tương tự
5 Bài toán tương tự về góc giữa các vector trong hình lập phương $ABCD.MNPQ$ (với $A$ dưới $M$, $B$ dưới $N$, $C$ dưới $P$, $D$ dưới $Q$):
**1.** Cho hình lập phương $ABCD.MNPQ$. Biết góc giữa $\overrightarrow{AC}$ và $\overrightarrow{MN}$ bằng $a^{\circ}$. Tính $a$?
A. $0$ B. $45$ C. $90$ D. $135$.
Đáp án đúng: B. $45$.
Lời giải ngắn gọn: $\overrightarrow{MN} = \overrightarrow{AB}$. Góc giữa $\overrightarrow{AC}$ và $\overrightarrow{MN}$ là góc giữa $\overrightarrow{AC}$ và $\overrightarrow{AB}$, là $\angle CAB$. Do $ABCD$ là hình vuông, $\angle CAB = 45^{\circ}$.
**2.** Cho hình lập phương $ABCD.MNPQ$. Tính góc giữa $\overrightarrow{AD}$ và $\overrightarrow{PN}$.
A. $0^{\circ}$ B. $45^{\circ}$ C. $90^{\circ}$ D. $180^{\circ}$.
Đáp án đúng: C. $90^{\circ}$.
Lời giải ngắn gọn: $\overrightarrow{AD} = \overrightarrow{MQ}$ và $\overrightarrow{PN} = \overrightarrow{CD}$. Góc giữa $\overrightarrow{AD}$ và $\overrightarrow{PN}$ là góc giữa $\overrightarrow{MQ}$ và $\overrightarrow{CD}$. Ta có $MQ \perp (ABCD)$, suy ra $MQ \perp CD$. Do đó, góc giữa $\overrightarrow{MQ}$ và $\overrightarrow{CD}$ là $90^{\circ}$.
**3.** Cho hình lập phương $ABCD.MNPQ$. Tính góc giữa $\overrightarrow{QN}$ và $\overrightarrow{AD}$.
A. $45^{\circ}$ B. $135^{\circ}$ C. $90^{\circ}$ D. $60^{\circ}$.
Đáp án đúng: B. $135^{\circ}$.
Lời giải ngắn gọn: $\overrightarrow{AD} = \overrightarrow{MQ}$. Góc cần tìm là góc giữa $\overrightarrow{QN}$ và $\overrightarrow{MQ}$. Trong hình vuông $MNPQ$, góc giữa $\overrightarrow{NQ}$ và $\overrightarrow{MQ}$ là $45^{\circ}$ (góc $\angle NQM$). Vì $\overrightarrow{QN} = -\overrightarrow{NQ}$, góc giữa $\overrightarrow{QN}$ và $\overrightarrow{MQ}$ là $180^{\circ} – 45^{\circ} = 135^{\circ}$.
**4.** Cho hình lập phương $ABCD.MNPQ$. Tính góc giữa $\overrightarrow{AB}$ và $\overrightarrow{CP}$.
A. $0^{\circ}$ B. $45^{\circ}$ C. $90^{\circ}$ D. $120^{\circ}$.
Đáp án đúng: C. $90^{\circ}$.
Lời giải ngắn gọn: $\overrightarrow{CP}$ là vector cạnh đứng, song song với $AM, BN, DQ$. $\overrightarrow{AB}$ là vector cạnh đáy. Cạnh đứng vuông góc với mặt đáy $(ABCD)$, do đó $\overrightarrow{CP}$ vuông góc với mọi vector nằm trong mặt đáy, bao gồm $\overrightarrow{AB}$. Góc là $90^{\circ}$.
**5.** Cho hình lập phương $ABCD.MNPQ$. Tính góc giữa $\overrightarrow{CD}$ và $\overrightarrow{PQ}$.
A. $0^{\circ}$ B. $45^{\circ}$ C. $90^{\circ}$ D. $180^{\circ}$.
Đáp án đúng: A. $0^{\circ}$.
Lời giải ngắn gọn: Cạnh $CD$ song song và bằng cạnh $PQ$ (vì $CDQP$ là hình chữ nhật và là hình vuông). Hơn nữa, $\overrightarrow{CD}$ và $\overrightarrow{PQ}$ cùng hướng. Do đó, góc giữa chúng là $0^{\circ}$.
