Bài toán gốc
Cho hàm số $y=\dfrac{x}{x-2}$. Xét tính đúng sai của các mệnh đề sau:
a) Tập xác định của hàm số là $D=\mathbb{R}$.
b) Bảng biến thiên của hàm số là
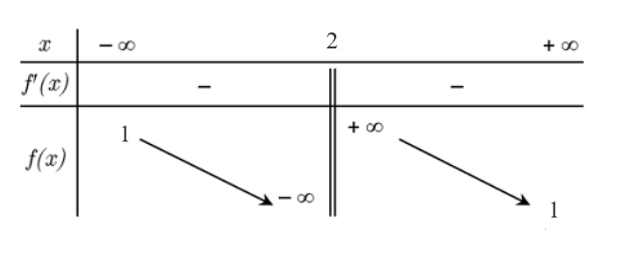
c) Giao điểm của đồ thị hàm số với trục tung là hai điểm phân biệt.
d) Gọi $A$ và $B$ là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số $y=\dfrac{x}{x-2}$. Khi đó độ dài đoạn $AB$ ngắn nhất bằng 16.
Lời giải:
(Sai) Tập xác định của hàm số là $D=\mathbb{R}$.
(Vì): Tập xác định của hàm số là $D=\mathbb{R}\backslash \left\{ 2 \right\}$.
Hàm số xác định khi $x-2\ne 0\Leftrightarrow x\ne 2$
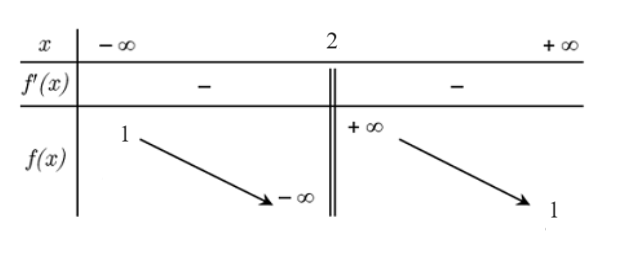
(Đúng) Bảng biến thiên của hàm số là
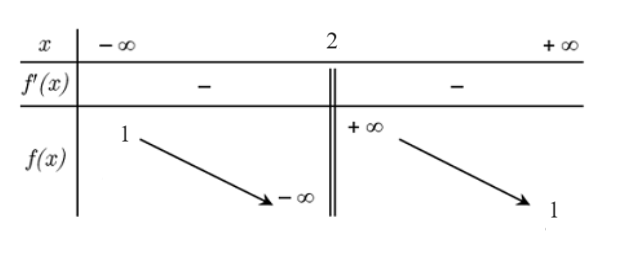
(Vì): Bảng biến thiên của hàm số là
(Sai) Giao điểm của đồ thị hàm số với trục tung là hai điểm phân biệt.
(Vì): Giao điểm của đồ thị hàm số với trục tung là gốc tọa độ.
Ta có: $f\left( 0 \right)=\dfrac{0}{0-2}=0\Rightarrow$ Đồ thị cắt trục tung tại một điểm duy nhất là gốc tọa độ.
(Sai) Gọi $A$ và $B$ là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số $y=\dfrac{x}{x-2}$. Khi đó độ dài đoạn $AB$ ngắn nhất bằng 16.
(Vì): Gọi $A$ và $B$ là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số $y=\dfrac{x}{x-2}$. Khi đó độ dài đoạn $AB$ ngắn nhất bằng 4.
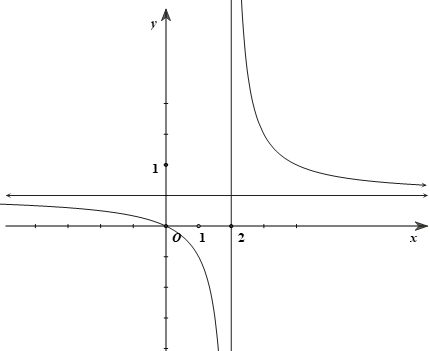
Hàm số $y=\dfrac{x}{x-2}$ có đồ thị $\left( C \right)$ như hình vẽ.
Gọi $A\left( a;\dfrac{a}{a-2} \right)$ và $B\left( b;\dfrac{b}{b-2} \right)$ là hai điểm thuộc hai nhánh của $\left( C \right)$ $\left( a{<}2{<}b \right)$. $\Rightarrow \overrightarrow{AB}=\left( b-a;\dfrac{b}{b-2}-\dfrac{a}{a-2} \right)=\left( b-a;\dfrac{b-a}{\left( b-2 \right)\left( 2-a \right)} \right)$
Áp dụng BĐT Côsi cho hai số dương $\left( b-2 \right)$ và $\left( 2-a \right)$ ta có: $\left( b-2 \right)\left( 2-a \right)\le \dfrac{{{\left( b-a \right)}^{2}}}{4}$. $\Rightarrow A{{B}^{2}}={{\left( b-a \right)}^{2}}+\dfrac{{{\left( b-a \right)}^{2}}}{{{\left[ \left( b-2 \right)\left( 2-a \right) \right]}^{2}}}\ge {{\left( b-a \right)}^{2}}+\dfrac{64}{{{\left( b-a \right)}^{2}}}\ge 16$
$\Rightarrow AB\ge 4$.
Dấu “ $=$ ” xảy ra $\Leftrightarrow \left\{ \begin{array}{l} b-2=2-a \\ {{\left( b-a \right)}^{2}}=\dfrac{64}{{{\left( b-a \right)}^{2}}} \end{array} \right.\Leftrightarrow \left\{ \begin{array}{l} a=2-\sqrt{2} \\ b=2+\sqrt{2} \end{array} \right.$
Vậy $A{{B}_{\min }}=4$.
Phân tích và Phương pháp giải
Dạng bài toán yêu cầu kiểm tra toàn diện các tính chất của hàm số hữu tỉ bậc nhất trên bậc nhất $y = \dfrac{ax+b}{cx+d}$, bao gồm Tập xác định, tính đơn điệu (qua Bảng biến thiên), giao điểm với các trục tọa độ, và đặc biệt là bài toán vận dụng tìm độ dài đoạn thẳng ngắn nhất nối hai điểm thuộc hai nhánh khác nhau của đồ thị. Phương pháp giải cho khoảng cách ngắn nhất là xác định tâm đối xứng $I$ của đồ thị và sử dụng công thức $A{{B}_{\min }}=2\sqrt{2|k|}$ hoặc áp dụng BĐT Cauchy sau khi chuyển hệ tọa độ về tâm đối xứng, trong đó $k$ là tử số sau khi chia $y$ về dạng $y = TCN + \dfrac{k}{x – TCĐ}$.
Bài toán tương tự
Thiết lập 5 bài toán tương tự dựa trên hàm số hữu tỉ bậc nhất trên bậc nhất, thay đổi các hệ số và tập trung vào các tính chất cơ bản và bài toán khoảng cách.
**1. Bài toán 1:** Cho hàm số $y=\dfrac{2x+1}{x+1}$. Xét tính đúng sai của các mệnh đề sau:
a) Hàm số có tiệm cận đứng $x=1$ và tiệm cận ngang $y=2$.
b) Hàm số đồng biến trên từng khoảng xác định của nó.\c) Giao điểm của đồ thị hàm số với trục hoành là điểm có tung độ khác 0.\d) Gọi $A$ và $B$ là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số. Độ dài đoạn $AB$ ngắn nhất bằng $2\sqrt{2}$.\n*Đáp án và Giải thích ngắn gọn:*\na) Sai. Tiệm cận đứng $x=-1$.
b) Đúng. $y’ = \dfrac{1}{(x+1)^2} > 0$.\c) Sai. Giao với trục hoành $y=0 \implies 2x+1=0 \implies x=-1/2$. Tung độ là 0.\d) Đúng. $y = 2 – \dfrac{1}{x+1}$. Tâm đối xứng $I(-1; 2)$. $|k| = 1$. $AB_{\min} = 2\sqrt{2|1|} = 2\sqrt{2}$.
**2. Bài toán 2 (Trắc nghiệm):** Gọi $A$ và $B$ là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số $y=\dfrac{3x-5}{x-1}$. Độ dài đoạn $AB$ ngắn nhất là:\A. 2\B. 4\C. $4\sqrt{2}$\D. 8\n*Đáp án đúng: B.*\n*Lời giải ngắn gọn:* Ta có $y = \dfrac{3x-5}{x-1} = 3 – \dfrac{2}{x-1}$. Tiệm cận đứng $x=1$. Hằng số $|k| = |-2| = 2$. Độ dài ngắn nhất $AB_{\min} = 2\sqrt{2|k|} = 2\sqrt{2(2)} = 4$.
**3. Bài toán 3 (Kiểm tra tính chất):** Cho hàm số $y=\dfrac{x+3}{2x+4}$. Mệnh đề nào sau đây là sai?\A. Hàm số có tiệm cận đứng $x=-2$ và tiệm cận ngang $y=1/2$.\B. Đồ thị hàm số có tâm đối xứng là $I(-2; 1/2)$.\C. Hàm số nghịch biến trên từng khoảng xác định.\D. Khoảng cách ngắn nhất giữa hai điểm thuộc hai nhánh khác nhau của đồ thị là $2\sqrt{2}$.\n*Đáp án đúng: D.*\n*Lời giải ngắn gọn:* Ta có $y = \dfrac{1}{2} + \dfrac{1}{2x+4}$. Tiệm cận $x=-2, y=1/2$. Tâm đối xứng $I(-2; 1/2)$. $y’ = \dfrac{-2}{(2x+4)^2} < 0$ nên hàm số nghịch biến. Mệnh đề A, B, C đúng. Khoảng cách ngắn nhất $AB_{\min} = 2\sqrt{2|1/2|} = 2$. Vì $2 \ne 2\sqrt{2}$, mệnh đề D là sai.\n
**4. Bài toán 4 (Tìm giá trị cụ thể):** Cho hàm số $y=\dfrac{x+1}{x-1}$. Nếu $M$ là điểm thuộc nhánh bên trái và $N$ là điểm thuộc nhánh bên phải của đồ thị. Tìm giá trị nhỏ nhất của độ dài đoạn $MN$.\n*Đáp án: 4.*\n*Lời giải ngắn gọn:* Ta có $y = 1 + \dfrac{2}{x-1}$. Tâm đối xứng $I(1; 1)$. Hằng số $|k|=2$. Giá trị nhỏ nhất của độ dài đoạn $MN$ là $M{N_{\min }} = 2\sqrt{2|2|} = 4$.
**5. Bài toán 5 (Trắc nghiệm tổng hợp):** Cho hàm số $y=\dfrac{3x+2}{x+2}$. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau:\(I) Tập xác định của hàm số là $\mathbb{R} \setminus \{-2\}$.\(II) Đồ thị hàm số không cắt trục tung.\(III) Hàm số luôn đồng biến trên từng khoảng xác định.\(IV) Độ dài đoạn thẳng ngắn nhất nối hai điểm thuộc hai nhánh khác nhau của đồ thị là $4\sqrt{2}$.\A. 1\B. 2\C. 3\D. 4\n*Đáp án đúng: C.*\n*Lời giải ngắn gọn:* \(I) Đúng.\(II) Sai. Cắt trục tung tại $(0, 1)$.\(III) Đúng. $y’ = \dfrac{4}{(x+2)^2} > 0$.\(IV) Đúng. $y = 3 – \dfrac{4}{x+2}$. $|k| = 4$. $AB_{\min} = 2\sqrt{2|4|} = 2\sqrt{8} = 4\sqrt{2}$.\Có 3 mệnh đề đúng: (I), (III), (IV).
