Một bác nông dân có ba tấm lưới B40, mỗi tấm dài $a = 8 \text{m}$ và muốn rào một mảnh vườn dọc theo bờ sông có dạng hình thang cân $ABCD$ như hình vẽ dưới đây biết rằng bờ sông là đường thẳng $CD$ không phải rào lưới.

Bài toán gốc

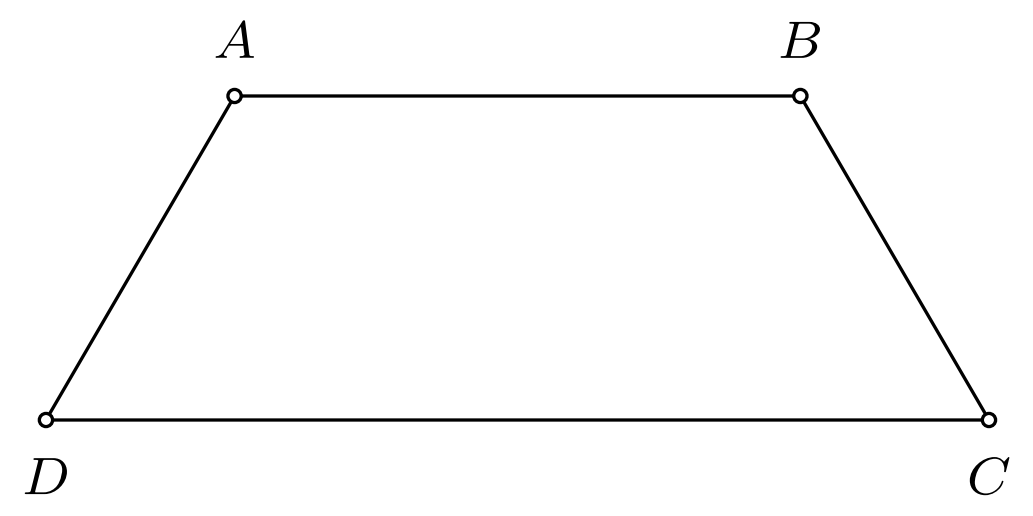
Một bác nông dân có ba tấm lưới B40, mỗi tấm dài $a = 8 \text{m}$ và muốn rào một mảnh vườn dọc theo bờ sông có dạng hình thang cân $ABCD$ như hình vẽ dưới đây biết rằng bờ sông là đường thẳng $CD$ không phải rào lưới. Hỏi bác nông dân đó có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu mét vuông?

A. $\dfrac{3\sqrt{3}}{4}$.B. $64\sqrt{3}$.C. $48 \sqrt{3}$.D. $8\sqrt{2}$.

Lời giải: Gọi $M, N$ lần lượt là hình chiếu vuông góc của $A, B$ lên $CD$.
Đặt $x = MD$, $(0 {<} x {<} 8)$ suy ra $AM = \sqrt{64 – x^2}$.
Diện tích của mảnh vườn hình thang cân là $S(x) = \dfrac{(AB + CD) AM}2 = (8 + x) \sqrt{64 – x^2}$.
Xét hàm số $f(x) = (8 + x) \sqrt{64 – x^2}$ trên khoảng $(0 {<} x {<} 8)$.
Đạo hàm $f^{\prime}(x) = – \dfrac{x \left(x + 8\right)}{\sqrt{64 – x^{2}}} + \sqrt{64 – x^{2}}$; $f^{\prime}(x) = 0$, ta được $x = 4$.
Lập bảng biến thiên

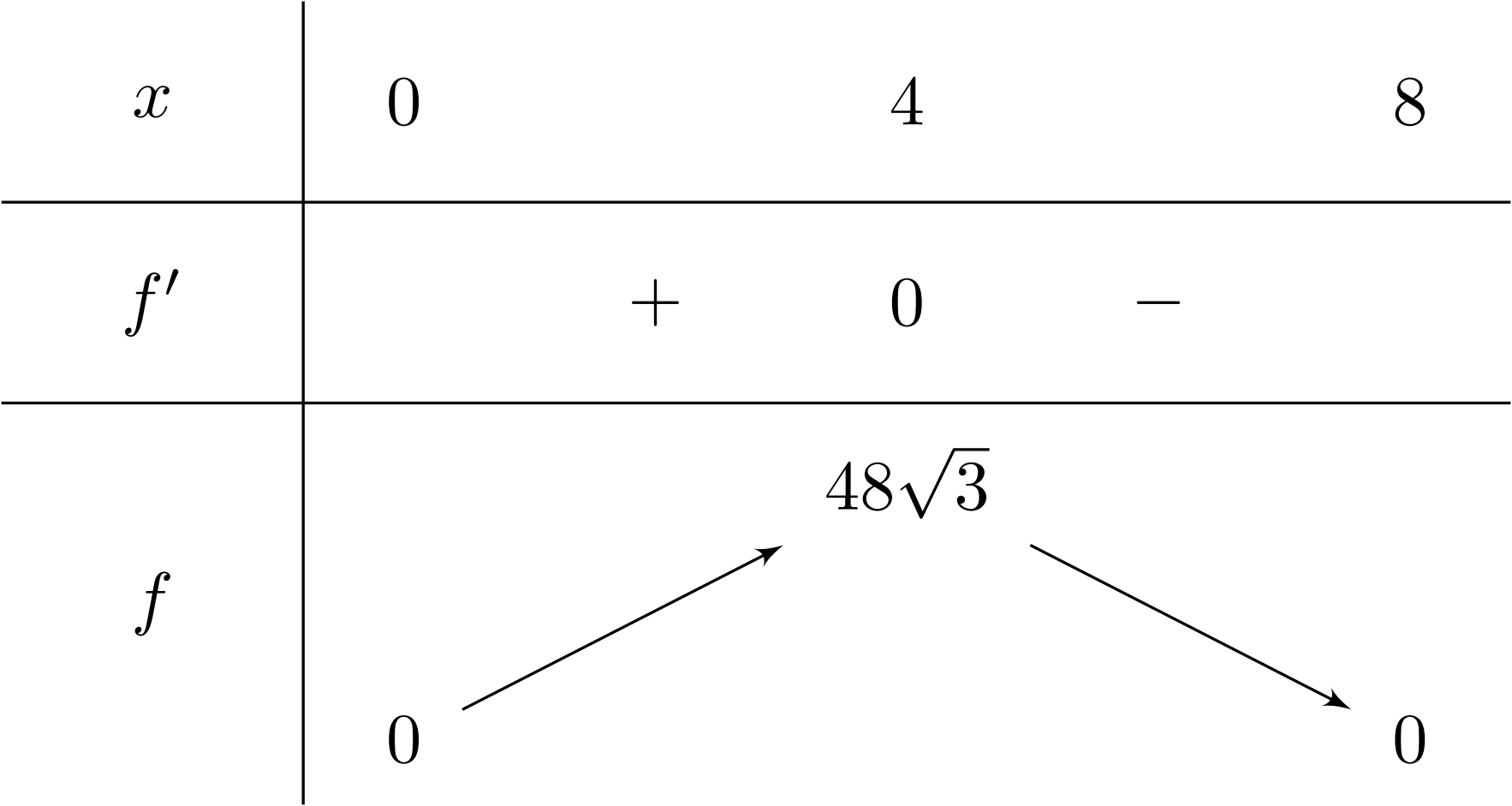
Từ bảng biến thiên suy ra $\max\limits_{x \in (0;8)} f(x) = f\left(4\right) = 48 \sqrt{3}$.
Vậy bác nông dân có thể rào được mảnh vườn có diện tích lớn nhất là $48 \sqrt{3}$ m$^2$.

Phân tích và Phương pháp giải

Đây là bài toán ứng dụng đạo hàm để giải quyết bài toán tối ưu hóa trong hình học, cụ thể là tìm diện tích lớn nhất của hình thang cân khi ba cạnh không giáp sông ($AB, AD, BC$) có tổng độ dài cố định (hoặc cố định từng cạnh như trong bài toán gốc: $AD=BC=AB=a$). Phương pháp giải bao gồm: 1. Đặt biến $x$ (thường là độ dài hình chiếu của cạnh bên lên đáy lớn). 2. Biểu diễn diện tích $S$ theo $x$. 3. Sử dụng công cụ đạo hàm để tìm điểm cực trị và xác định giá trị lớn nhất của hàm diện tích $S(x)$ trên miền xác định.

Bài toán tương tự

Tuyệt vời! Dưới đây là 5 bài toán tương tự cùng dạng và phương pháp giải:

**Câu 1:** Một bác nông dân có ba tấm lưới B40, mỗi tấm dài $a = 6 \text{m}$ và muốn rào một mảnh vườn dọc theo bờ sông có dạng hình thang cân $ABCD$ (bờ sông là $CD$). Biết rằng ba cạnh $AB, AD, BC$ được rào bằng các tấm lưới này ($AD=BC=AB=6\text{m}$). Hỏi bác nông dân đó có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu mét vuông? \n\nA. $9\sqrt{3}$. B. $18\sqrt{2}$. C. $27\sqrt{3}$. D. $36$. \nĐáp án đúng: C.\nLời giải ngắn gọn: Gọi $x$ là hình chiếu của cạnh bên lên đáy lớn ($0 < x < 6$). Chiều cao $h = \sqrt{36 - x^2}$. Diện tích $S(x) = (6+x)\sqrt{36-x^2}$. Xét $S'(x)=0$ ta được $x=3$. $S_{max} = S(3) = (6+3)\sqrt{36-9} = 9\sqrt{27} = 27\sqrt{3}$ m$^2$. **Câu 2:** Nếu bác nông dân trong bài toán trên sử dụng các tấm lưới dài $a=12\text{m}$ cho mỗi cạnh ($AD=BC=AB=12\text{m}$), hỏi diện tích lớn nhất có thể rào được là bao nhiêu mét vuông? \n\nA. $72\sqrt{3}$. B. $108\sqrt{3}$. C. $144$. D. $81\sqrt{2}$. \nĐáp án đúng: B.\nLời giải ngắn gọn: Đặt $x$ là hình chiếu ($0 < x < 12$). $S(x) = (12+x)\sqrt{144-x^2}$. $S'(x) = 0 \implies x=6$. $S_{max} = S(6) = (12+6)\sqrt{144-36} = 18\sqrt{108} = 18 \cdot 6\sqrt{3} = 108\sqrt{3}$ m$^2$. **Câu 3:** Một người muốn rào một khu đất hình chữ nhật dọc theo bờ sông (không rào phía bờ sông). Tổng độ dài hàng rào là $32\text{m}$. Hỏi diện tích lớn nhất của khu đất có thể rào được là bao nhiêu mét vuông?\n\nA. $128$. B. $64$. C. $256$. D. $96$. \nĐáp án đúng: A.\nLời giải ngắn gọn: Gọi $x$ là chiều rộng (cạnh vuông góc với sông), $y$ là chiều dài (cạnh song song với sông). Ta có $2x+y=32 \implies y=32-2x$. Diện tích $S(x) = x(32-2x) = 32x – 2x^2$. $S'(x) = 32 – 4x$. $S'(x)=0 \implies x=8$. $S_{max} = S(8) = 8(32-16) = 128$ m$^2$. **Câu 4:** Một bác nông dân có ba tấm lưới B40, mỗi tấm dài $a = 5 \text{m}$ và muốn rào một mảnh vườn dọc theo bờ sông có dạng hình thang cân $ABCD$ ($AD=BC=AB=5\text{m}$). Hỏi bác nông dân đó có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu mét vuông? \n\nA. $25\sqrt{3}/4$. B. $75\sqrt{3}/4$. C. $25\sqrt{2}$. D. $50$. \nĐáp án đúng: B.\nLời giải ngắn gọn: Đặt $x$ là hình chiếu ($0 < x < 5$). $S(x) = (5+x)\sqrt{25-x^2}$. $S'(x)=0 \implies -2x^2 - 5x + 25 = 0$. Vì $x>0$, ta chọn $x=2.5$. $S_{max} = S(2.5) = (5+2.5)\sqrt{25-6.25} = 7.5 \cdot \sqrt{18.75} = \dfrac{15}{2} \cdot \dfrac{5\sqrt{3}}{2} = \dfrac{75\sqrt{3}}{4}$ m$^2$.

**Câu 5:** Một người nông dân có tổng cộng $30\text{m}$ hàng rào để rào ba cạnh $AB, AD, BC$ của một mảnh vườn hình thang cân dọc bờ sông $CD$. Nếu người nông dân quyết định rào ba cạnh này có độ dài bằng nhau ($AD=BC=AB$), hỏi diện tích lớn nhất có thể đạt được là bao nhiêu? \n\nA. $15\sqrt{3}$. B. $75\sqrt{3}$. C. $50\sqrt{3}$. D. $100$. \nĐáp án đúng: B.\nLời giải ngắn gọn: Do $AD=BC=AB$, nên $3\cdot AD = 30\text{m}$, suy ra $AD=BC=AB=10\text{m}$. Đặt $x$ là hình chiếu ($0 < x < 10$). Diện tích $S(x) = (10+x)\sqrt{100-x^2}$. $S'(x)=0 \implies x=5$. $S_{max} = S(5) = (10+5)\sqrt{100-25} = 15\sqrt{75} = 75\sqrt{3}$ m$^2$.