Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:

Bài toán gốc

Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:

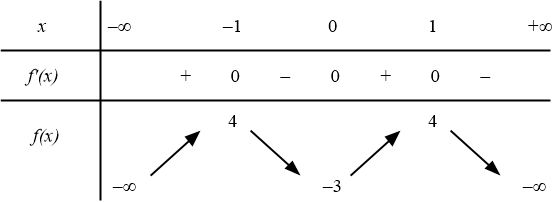
Số giá trị nguyên $m$ để phương trình $f(x)=m+4$ có 4 nghiệm?

A. $9$.B. $4$.C. $3$.D. $6$.

Phân tích và Phương pháp giải

Dạng bài toán nhận biết số nghiệm của phương trình $f(x)=k$ dựa vào bảng biến thiên (BBT) của hàm số $y=f(x)$. Số nghiệm của phương trình $f(x)=k$ bằng số giao điểm của đồ thị hàm số $y=f(x)$ và đường thẳng ngang $y=k$. Để phương trình có 4 nghiệm phân biệt, hàm số $f(x)$ phải có 3 cực trị, tạo ra hình dạng chữ ‘W’ (hoặc ‘M’ ngược). Khi đó, $k$ phải nằm strictly giữa giá trị cực tiểu địa phương $m_{CT}$ và giá trị cực đại địa phương thấp hơn $M_{CĐ, thấp}$. Cụ thể, nếu các cực trị là $M_1, m, M_2$, thì điều kiện là $ ext{min}(M_1, M_2) < k < ext{max}(M_1, M_2)$ nếu $m$ là cực đại, hoặc $m < k < M_{\text{min}}$ nếu $m$ là cực tiểu.

Bài toán tương tự

1. Cho hàm số $y=f(x)$ có bảng biến thiên (giả định hàm số có 3 cực trị, với các giá trị cực trị là cực đại $M=7$ và cực tiểu $m=2$). Số giá trị nguyên $m$ để phương trình $f(x)=m+5$ có 4 nghiệm phân biệt là:
A. 2. B. 3. C. 4. D. 5.
Đáp án đúng: C. Lời giải ngắn gọn: Để phương trình có 4 nghiệm phân biệt, $k=m+5$ phải thỏa mãn $2 < k < 7$. Ta có $2 < m+5 < 7 \Leftrightarrow -3 < m < 2$. Vì $m$ nguyên, $m \in \{-2, -1, 0, 1\}$. Có 4 giá trị nguyên $m$. 2. Cho hàm số $y=f(x)$ có bảng biến thiên (giả định hàm số có 3 cực trị, với các giá trị cực trị là cực đại $M=6$ và cực tiểu $m=-2$). Số giá trị nguyên $m$ để phương trình $f(x)=2m$ có 4 nghiệm phân biệt là:
A. 5. B. 4. C. 3. D. 2.
Đáp án đúng: C. Lời giải ngắn gọn: Để phương trình có 4 nghiệm phân biệt, $k=2m$ phải thỏa mãn $-2 < k < 6$. Ta có $-2 < 2m < 6 \Leftrightarrow -1 < m < 3$. Vì $m$ nguyên, $m \in \{0, 1, 2\}$. Có 3 giá trị nguyên $m$. 3. Cho hàm số $y=f(x)$ có bảng biến thiên (giả định hàm số có 3 cực trị, với các giá trị cực trị là cực đại $M=3$ và cực tiểu $m=0$). Số giá trị nguyên $m$ để phương trình $f(x)=m-2$ có 4 nghiệm phân biệt là:
A. 4. B. 3. C. 2. D. 1.
Đáp án đúng: C. Lời giải ngắn gọn: Để phương trình có 4 nghiệm phân biệt, $k=m-2$ phải thỏa mãn $0 < k < 3$. Ta có $0 < m-2 < 3 \Leftrightarrow 2 < m < 5$. Vì $m$ nguyên, $m \in \{3, 4\}$. Có 2 giá trị nguyên $m$. 4. Cho hàm số $y=f(x)$ có bảng biến thiên (giả định hàm số có 3 cực trị, với các giá trị cực trị là cực đại $M=8$ và cực tiểu $m=-4$). Số giá trị nguyên $m$ để phương trình $f(x)=3m+1$ có 4 nghiệm phân biệt là:
A. 2. B. 3. C. 4. D. 5.
Đáp án đúng: C. Lời giải ngắn gọn: Để phương trình có 4 nghiệm phân biệt, $k=3m+1$ phải thỏa mãn $-4 < k < 8$. Ta có $-4 < 3m+1 < 8 \Leftrightarrow -5 < 3m < 7 \Leftrightarrow -5/3 < m < 7/3$. Vì $m$ nguyên, $m \in \{-1, 0, 1, 2\}$. Có 4 giá trị nguyên $m$. 5. Cho hàm số $y=f(x)$ có bảng biến thiên (giả định hàm số có 3 cực trị, với các giá trị cực trị là cực đại $M=5$ và cực tiểu $m=-5$). Số giá trị nguyên $m$ để phương trình $f(x)=m^2+m$ có 4 nghiệm phân biệt là:
A. 3. B. 4. C. 5. D. 6.
Đáp án đúng: B. Lời giải ngắn gọn: Để phương trình có 4 nghiệm phân biệt, $k=m^2+m$ phải thỏa mãn $-5 < k < 5$. Ta có $-5 < m^2+m < 5$.
Xét $m^2+m < 5 \Leftrightarrow m^2+m-5 < 0$. Nghiệm của $m^2+m-5=0$ là $m = \frac{-1 \pm \sqrt{21}}{2}$ (xấp xỉ $-2.79$ và $1.79$). Do đó $-2.79 < m < 1.79$.
Xét $m^2+m > -5 \Leftrightarrow m^2+m+5 > 0$. Delta $\Delta = 1 – 4(5) = -19 < 0$. Bất phương trình này luôn đúng với mọi $m$.
Kết hợp điều kiện, ta cần $-2.79 < m < 1.79$. Vì $m$ nguyên, $m \in \{-2, -1, 0, 1\}$. Có 4 giá trị nguyên $m$.