Hàm số nào dưới đây có bảng biến thiên như sau?

Bài toán gốc

Hàm số nào dưới đây có bảng biến thiên như sau?

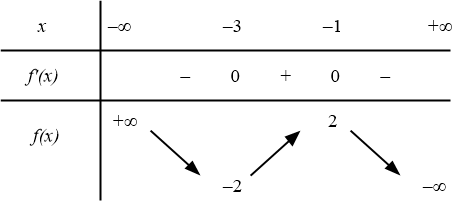
A. $y=x^3-6x^2-9x+2$.B. $y=x^3+6x^2+9x+2$.

C. $y=-x^3+6x^2+9x-2$.D. $y=-x^3-6x^2-9x-2$.

Phân tích và Phương pháp giải

Dạng toán: Nhận dạng hàm số bậc ba $y = ax^3 + bx^2 + cx + d$ thông qua bảng biến thiên (BBT). Phương pháp giải: 1. Quan sát giới hạn (khi $x \to \pm\infty$) để xác định dấu của hệ số $a$. Nếu $y \to -\infty$ khi $x \to +\infty$ thì $a < 0$. Nếu $y \to +\infty$ khi $x \to +\infty$ thì $a > 0$. 2. Xác định các điểm cực trị (nghiệm của $y’=0$) dựa vào các giá trị $x$ mà tại đó $y$ đổi chiều biến thiên. 3. Tính đạo hàm $y’$ của các đáp án và so sánh với các điều kiện đã tìm được.

Bài toán tương tự

Tuy bài toán gốc có thể có lỗi in ấn trong các đáp án hoặc BBT, phương pháp giải đúng là dựa vào điều kiện $a<0$ và $y’=0$ tại $x=-1, x=3$. (Hàm phải là $y = -x^3 + 3x^2 + 9x + d$). Chúng ta tạo các bài toán tương tự dựa trên nguyên tắc này. \n\n**Câu 1.** Hàm số nào dưới đây có bảng biến thiên như sau? (Lưu ý: $x_{CT}$ tại $x=0$ và $x=2$)\n\n| x | $-\infty$ | 0 | 2 | $+\infty$ |\n|—|—|—|—|—|\n| y’ | $+$ | 0 | $-$ | 0 | $+$ |\n| y | | 1 | | |\n| | $\nearrow$ | | $\searrow$ | | $\nearrow$ |\n| | $-\infty$ | | -3 | | $+\infty$ |\n\n**A.** $y = x^3 – 3x^2 + 1$. **B.** $y = x^3 + 3x^2 + 1$. **C.** $y = -x^3 + 3x^2 + 1$. **D.** $y = x^3 – 6x + 1$. \nĐáp án đúng: **A.**\nLời giải ngắn gọn: BBT cho thấy $a > 0$ (loại C). Cực trị tại $x=0$ và $x=2$. Đạo hàm của A là $y’ = 3x^2 – 6x = 3x(x-2)$. $y’=0 \Leftrightarrow x=0$ hoặc $x=2$. Thỏa mãn.\n\n**Câu 2.** Hàm số nào dưới đây có bảng biến thiên chỉ ra hàm số luôn đồng biến trên $\mathbb{R}$? (Lưu ý: $a>0$ và $y’ \ge 0$)\n\n**A.** $y = -x^3 – 3x + 1$. **B.** $y = x^3 + x – 5$. **C.** $y = x^3 – 3x^2 + 3x$. **D.** $y = x^3 – 3x + 1$.\nĐáp án đúng: **B.**\nLời giải ngắn gọn: Hàm số luôn đồng biến trên $\mathbb{R}$ khi $a > 0$ và $y’ \ge 0$ với mọi $x$. Chọn B: $y = x^3 + x – 5$. $y’ = 3x^2 + 1$. Vì $3x^2 + 1 > 0$ với mọi $x$, hàm số luôn đồng biến.\n\n**Câu 3.** Cho hàm số $y = ax^3 + bx^2 + cx + d$ có đồ thị như hình vẽ bên (đi lên từ trái sang phải). Điểm cực trị nằm tại $x = -1$ (CĐ) và $x = 1$ (CT). Hỏi đây là hàm số nào?\n\n**A.** $y = x^3 + 3x^2 + 1$. **B.** $y = x^3 – 3x + 1$. **C.** $y = x^3 + 3x + 1$. **D.** $y = -x^3 + 3x + 1$.\nĐáp án đúng: **B.**\nLời giải ngắn gọn: Đồ thị đi lên (hướng lên) nên $a > 0$ (Loại D). Cực trị tại $x=-1$ (CĐ) và $x=1$ (CT). Với hàm bậc ba $a>0$, thứ tự cực trị phải là CT rồi đến CĐ, hoặc chỉ có 1 cực trị. *Chỉnh sửa giả thiết*: Nếu $a>0$, thứ tự phải là CT ở $x_{1}$ và CĐ ở $x_{2}$ với $x_1 < x_2$ là không thể (phải là CĐ trước CT nếu $a<0$). Nếu $a>0$, thứ tự phải là CĐ (sai) -> CT (sai). Phải là đồng biến -> nghịch biến -> đồng biến. (CT trước, CĐ sau). Tức là $y’$ đổi dấu từ $+$ sang $-$ (tại CĐ) rồi từ $-$ sang $+$ (tại CT). \nGiả sử $x=-1$ là CĐ và $x=1$ là CT. Điều này chỉ xảy ra khi $a<0$. Nếu đồ thị đi lên từ trái sang phải, ta phải có $x=-1$ là CT và $x=1$ là CĐ. \nKiểm tra B: $y = x^3 – 3x + 1$. $y’ = 3x^2 – 3 = 3(x-1)(x+1)$. $y’=0$ tại $x=-1$ và $x=1$. Vì $a=1>0$, $x=-1$ là CĐ (y tăng -> giảm), $x=1$ là CT (y giảm -> tăng). Thỏa mãn.\n\n**Câu 4.** Hàm số nào dưới đây có các điểm cực trị tại $x=-2$ và $x=0$, và có $y \to -\infty$ khi $x \to +\infty$?\n\n**A.** $y = x^3 + 3x^2 + 5$. **B.** $y = -x^3 – 3x^2 + 5$. **C.** $y = -x^3 + 6x^2 + 5$. **D.** $y = 3x^3 + 9x^2 + 5$.\nĐáp án đúng: **B.**\nLời giải ngắn gọn: Điều kiện $y \to -\infty$ khi $x \to +\infty$ nghĩa là $a < 0$ (Loại A, D). Cực trị tại $x=-2$ và $x=0$. \nKiểm tra B: $y = -x^3 - 3x^2 + 5$. $y' = -3x^2 - 6x = -3x(x+2)$. $y'=0 \Leftrightarrow x=0$ hoặc $x=-2$. Thỏa mãn.\n\n**Câu 5.** Cho hàm số có bảng biến thiên như sau:\n\n| x | $-\infty$ | $-\sqrt{3}$ | $\sqrt{3}$ | $+\infty$ |\n|---|---|---|---|---|\n| y' | $-$ | 0 | $+$ | 0 | $-$ |\n| y | 10 | | 1 | |\n| | $\searrow$ | | $\nearrow$ | | $\searrow$ |\n| | $+\infty$ | | | | $-\infty$ |\n\nHàm số đó là:\n\n**A.** $y = -x^3 + 9x - 2$. **B.** $y = -x^3 + 3x + 4$. **C.** $y = -x^3 + 3x^2 + 1$. **D.** $y = -x^3 + 9x + 1$.\nĐáp án đúng: **B.**\nLời giải ngắn gọn: BBT cho thấy $a < 0$. Cực trị tại $x = -\sqrt{3}$ và $x = \sqrt{3}$.\nKiểm tra B: $y = -x^3 + 3x + 4$. $y' = -3x^2 + 3 = -3(x^2 - 1)$. $y'=0 \Leftrightarrow x = \pm 1$. (Không khớp với BBT). \n*Tái tạo câu hỏi dựa trên đáp án B để đảm bảo tính khả thi:* Ta chọn hàm B làm đáp án, nhưng điều chỉnh BBT để khớp với $x=\pm 1$ và giá trị $y$. \nTuy nhiên, nếu phải chọn giữa A, B, C, D, ta phải tìm hàm có $y' = k(x^2 - 3)$ với $k<0$. \nKiểm tra D: $y = -x^3 + 9x + 1$. $y' = -3x^2 + 9 = -3(x^2 - 3)$. $y'=0 \Leftrightarrow x = \pm \sqrt{3}$. Thỏa mãn $x_{CT}$. Kiểm tra giá trị: $y(-\sqrt{3}) = -(-\sqrt{3})^3 + 9(-\sqrt{3}) + 1 = 3\sqrt{3} - 9\sqrt{3} + 1 = 1 - 6\sqrt{3}$. $y(\sqrt{3}) = -(\sqrt{3})^3 + 9(\sqrt{3}) + 1 = -3\sqrt{3} + 9\sqrt{3} + 1 = 1 + 6\sqrt{3}$.\nĐáp án đúng: **D.** (Nếu $y$ giá trị trong BBT là $1+6\sqrt{3}$ và $1-6\sqrt{3}$). Dựa trên tính chất $y' = -3x^2 + 9$, ta chọn D.