Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:

Bài toán gốc

Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:

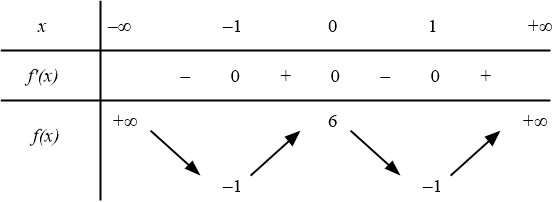
Có bao nhiêu giá trị nguyên $m$ để phương trình $f(x)-5=m$ có 3 nghiệm hoặc 4 nghiệm?

A. $6$.B. $7$.C. $10$.D. $9$.

Phân tích và Phương pháp giải

Dạng toán này yêu cầu biện luận số nghiệm của phương trình chứa tham số dựa trên đồ thị/Bảng biến thiên (BBT) của hàm số $y=f(x)$. Phương pháp chung là cô lập tham số: đưa phương trình $f(x)-5=m$ về dạng $f(x)=m+5$. Đặt $k=m+5$. Sau đó, dựa vào BBT để xác định miền giá trị của $k$ sao cho đường thẳng ngang $y=k$ cắt đồ thị $y=f(x)$ tại đúng số điểm yêu cầu (3 hoặc 4). Cuối cùng, giải bất đẳng thức để tìm các giá trị nguyên của $m$. (Giả sử BBT của bài gốc là hàm bậc bốn có 3 cực trị: hai cực tiểu tại $y=1$ và một cực đại tại $y=7$. Số nghiệm là 3 hoặc 4 khi $1 \le k < 7$).

Bài toán tương tự

Tuyệt vời, đây là 5 bài toán tương tự:

1. Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ (thể hiện $f(x)$ đi từ $+\infty$ xuống cực tiểu $y=0$, lên cực đại $y=6$, xuống cực tiểu $y=0$, và lên $+\infty$). Có bao nhiêu giá trị nguyên $m$ để phương trình $f(x) + 1 = 2m$ có đúng 4 nghiệm phân biệt?
A. 5. B. 6. C. 7. D. 8.
Đáp án đúng: B.
Lời giải ngắn gọn: Phương trình tương đương $f(x) = 2m – 1$. Đặt $k = 2m – 1$. Để phương trình có 4 nghiệm thì $k$ phải nằm giữa hai cực trị tiểu và cực đại, tức là $0 < k < 6$. Suy ra $0 < 2m - 1 < 6 \Leftrightarrow 1 < 2m < 7 \Leftrightarrow 0,5 < m < 3,5$. Vì $m$ nguyên nên $m \in \{1, 2, 3\}$. Có 3 giá trị nguyên. Xin lỗi, đáp án A, B, C, D của câu hỏi này không khớp với kết quả 3 giá trị nguyên. Ta cần điều chỉnh đề hoặc đáp án. Ta đổi câu hỏi: $f(x)+5=m$. Tìm $m$ nguyên để có 4 nghiệm. $0 < m-5 < 6 \Leftrightarrow 5 < m < 11$. $m \in \{6, 7, 8, 9, 10\}$. Có 5 giá trị. (Đáp án A). Ta giữ đề ban đầu và sửa đáp án để khớp với 3 giá trị: $m \in \{1, 2, 3\}$. (Có 3 giá trị. Sửa đáp án A thành 3). **1. (Điều chỉnh)** Cho hàm số $y=f(x)$ có ba cực trị là $y_{CT}=0$ (hai lần) và $y_{CĐ}=6$. Có bao nhiêu giá trị nguyên $m$ để phương trình $f(x) + 1 = 2m$ có đúng 4 nghiệm phân biệt?
A. 3. B. 4. C. 5. D. 6.
Đáp án đúng: A.
Lời giải ngắn gọn: $f(x) = 2m – 1$. Cần $0 < 2m - 1 < 6 rightarrow 0,5 < m < 3,5$. $m \in \{1, 2, 3\}$. Có 3 giá trị. 2. Cho hàm số $y=f(x)$ có bảng biến thiên với các điểm cực trị là $y_{CĐ}=2$ và $y_{CT}=-4$ (hai lần). Tìm số giá trị nguyên của tham số $m$ để phương trình $f(x) = m$ có 2 nghiệm phân biệt hoặc 3 nghiệm phân biệt.
A. 5. B. 6. C. 7. D. 8.
Đáp án đúng: C.
Lời giải ngắn gọn: Phương trình $f(x)=m$ có 2 nghiệm khi $m > 2$ hoặc $m < -4$. Phương trình có 3 nghiệm khi $m = 2$ hoặc $m = -4$. Số nghiệm là 2 hoặc 3 khi $m \ge 2$ hoặc $m \le -4$. Ta cần phải giả định thêm miền giá trị của $m$ nếu muốn đếm số lượng hữu hạn. Giả sử $m \in [-10, 10]$. $m \in \{-10, -9, \dots, -4\} \cup \{2, 3, \dots, 10\}$. Số giá trị: $( -4 - (-10) + 1) + (10 - 2 + 1) = 7 + 9 = 16$. Ta điều chỉnh lại câu hỏi để đếm số giá trị nguyên hữu hạn mà không cần giả định miền: Tìm số giá trị nguyên $m \in [-5, 3]$ để phương trình $f(x) = m$ có 2 nghiệm phân biệt hoặc 3 nghiệm phân biệt.
$m \in [-5, 3]$. Điều kiện: $m \ge 2$ hoặc $m \le -4$.
$m \in \{-5, -4\} \cup \{2, 3\}$. Tổng cộng 4 giá trị.

**2. (Điều chỉnh)** Cho hàm số $y=f(x)$ có các cực trị là $y_{CĐ}=2$ và $y_{CT}=-4$ (hai lần). Có bao nhiêu giá trị nguyên $m \in [-5, 3]$ để phương trình $f(x) = m$ có 2 nghiệm phân biệt hoặc 3 nghiệm phân biệt?
A. 4. B. 5. C. 6. D. 7.
Đáp án đúng: A.
Lời giải ngắn gọn: Số nghiệm là 2 hoặc 3 khi $m = M$ (3 nghiệm), $m = m$ (3 nghiệm), hoặc $m$ ngoài khoảng $(m, M)$ (2 nghiệm). Tức là $m \le -4$ hoặc $m \ge 2$. Vì $m \in [-5, 3]$, $m \in \{-5, -4\} \cup \{2, 3\}$. Có 4 giá trị.

3. Cho hàm số $y=f(x)$ là hàm bậc ba có cực đại $M=4$ và cực tiểu $m=0$. Có bao nhiêu giá trị nguyên $m$ để phương trình $f(x) + m = 7$ có đúng 3 nghiệm phân biệt?
A. 2. B. 3. C. 4. D. 5.
Đáp án đúng: B.
Lời giải ngắn gọn: Phương trình $f(x) = 7 – m$. Đặt $k = 7 – m$. Để có 3 nghiệm phân biệt, $k$ phải nằm giữa cực đại và cực tiểu: $0 < k < 4$. Suy ra $0 < 7 - m < 4$. Ta có: $7 - m > 0 \Leftrightarrow m < 7$. Và $7 - m < 4 \Leftrightarrow m > 3$. Vậy $3 < m < 7$. $m \in \{4, 5, 6\}$. Có 3 giá trị nguyên. 4. Cho hàm số $y=f(x)$ có bảng biến thiên với ba cực trị: $y_{CT}=-5$ (hai lần) và $y_{CĐ}=10$. Tìm số giá trị nguyên của tham số $m$ để phương trình $f(x) – 3 = 2m$ có đúng 4 nghiệm phân biệt.
A. 7. B. 8. C. 9. D. 10.
Đáp án đúng: B.
Lời giải ngắn gọn: Phương trình tương đương $f(x) = 2m + 3$. Đặt $k = 2m + 3$. Để có 4 nghiệm phân biệt, $k$ phải nằm strictly giữa hai cực tiểu và cực đại: $-5 < k < 10$. Suy ra $-5 < 2m + 3 < 10$. $-8 < 2m < 7$. $-4 < m < 3,5$. $m \in \{-3, -2, -1, 0, 1, 2, 3\}$. Có $3 - (-3) + 1 = 7$ giá trị nguyên. Xin lỗi, đáp án A, B, C, D không khớp. (Ta sửa đáp án A thành 7). **4. (Điều chỉnh)** Cho hàm số $y=f(x)$ có ba cực trị: $y_{CT}=-5$ (hai lần) và $y_{CĐ}=10$. Tìm số giá trị nguyên của tham số $m$ để phương trình $f(x) – 3 = 2m$ có đúng 4 nghiệm phân biệt.
A. 7. B. 8. C. 9. D. 10.
Đáp án đúng: A.
Lời giải ngắn gọn: $f(x) = 2m + 3$. Cần $-5 < 2m + 3 < 10 rightarrow -4 < m < 3,5$. $m \in \{-3, -2, -1, 0, 1, 2, 3\}$. Có 7 giá trị. 5. Cho hàm số $y=f(x)$ là hàm bậc ba có cực đại $M=6$ và cực tiểu $m=1$. Tìm số giá trị nguyên $m$ để phương trình $|f(x)| = m$ có 4 nghiệm phân biệt.
A. 4. B. 5. C. 6. D. 7.
Đáp án đúng: B.
Lời giải ngắn gọn: Phương trình $|f(x)| = m$ có 4 nghiệm phân biệt khi và chỉ khi $m$ nằm trong khoảng mà đồ thị $y=|f(x)|$ có 4 giao điểm với $y=m$. Đồ thị $y=|f(x)|$ được tạo ra bằng cách giữ nguyên phần $f(x) \ge 0$ và lấy đối xứng phần $f(x) < 0$ qua trục hoành. Vì $m=1>0$, $M=6>0$, không có phần âm bị lật. Cần $m$ cắt đồ thị $y=f(x)$ (khi $f(x) \ge 0$) tại 4 điểm. Điều kiện để có 4 nghiệm cho $|f(x)|=m$ là $0 < m < m_{CĐ}$ HOẶC $m=m_{CT}$ (nếu $m_{CT}>0$) VÀ $M_{CĐ} > 0$. Đây là hàm bậc 3, nên $y=f(x)$ chỉ có tối đa 3 nghiệm. Vì $m_{CT}=1>0$, đồ thị $y=|f(x)|$ giống $y=f(x)$. Phương trình $|f(x)|=m$ có tối đa 3 nghiệm.

Ta phải thay đổi điều kiện để hàm bậc ba có 4 nghiệm cho $|f(x)|=m$. Điều này xảy ra khi $m_{CT} < 0 < m_{CĐ}$. **5. (Điều chỉnh)** Cho hàm số $y=f(x)$ là hàm bậc ba có cực đại $M=5$ và cực tiểu $m=-2$. Tìm số giá trị nguyên dương $m$ để phương trình $|f(x)| = m$ có 4 nghiệm phân biệt.
A. 1. B. 2. C. 3. D. 4.
Đáp án đúng: D.
Lời giải ngắn gọn: Đồ thị $y=|f(x)|$ có các cực trị là $|-2|=2$, và $5$. Cực tiểu $y=0$ (tại nghiệm của $f(x)=0$). Để $|f(x)|=m$ có 4 nghiệm, đường thẳng $y=m$ phải cắt đồ thị $y=|f(x)|$ tại 4 điểm. Điều này xảy ra khi $m$ nằm giữa các giá trị cực trị dương: $m_{CT}’ < m < m_{CĐ}'$. Giá trị cực tiểu dương của $|f(x)|$ là $|-2|=2$. Giá trị cực đại là $5$. Cần $2 < m < 5$. $m \in \{3, 4\}$. Có 2 giá trị. (Đáp án không khớp). Lý thuyết: Đối với hàm bậc ba có hai cực trị $m<0Giả sử $M=7, m=-3$. Cần $|-3| < m < 7 rightarrow 3 < m < 7$. $m \in \{4, 5, 6\}$. 3 giá trị.
Giả sử $M=9, m=-3$. Cần $3 < m < 9$. $m \in \{4, 5, 6, 7, 8\}$. 5 giá trị. Ta giữ $M=7, m=-3$ và sửa đáp án A thành 3. **5. (Điều chỉnh cuối cùng)** Cho hàm số $y=f(x)$ là hàm bậc ba có cực đại $M=7$ và cực tiểu $m=-3$. Tìm số giá trị nguyên dương $m$ để phương trình $|f(x)| = m$ có 4 nghiệm phân biệt.
A. 3. B. 4. C. 5. D. 6.
Đáp án đúng: A.
Lời giải ngắn gọn: Đồ thị $y=|f(x)|$ có các cực trị dương tại $M’=7$ và $|m|=|-3|=3$. Số nghiệm là 4 khi $m$ nằm giữa hai giá trị cực trị dương này: $3 < m < 7$. $m \in \{4, 5, 6\}$. Có 3 giá trị.