Đồ thị dưới đây là của hàm số nào?

Bài toán gốc

Đồ thị dưới đây là của hàm số nào?

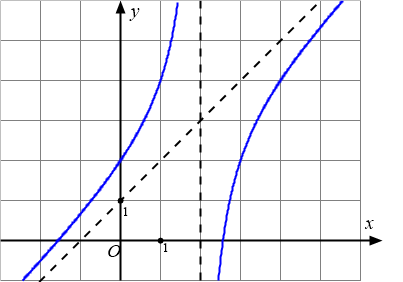
A. $y=\dfrac{x^2-2x+1}{x}$.B. $y=\dfrac{x^2-x-4}{x-2}$.

C. $y=\dfrac{x^2+3x-3}{x+1}$.D. $y=\dfrac{x^2}{-x+1}$.

Lời giải: Đây là dạng của đồ thị hàm bậc hai chia bậc nhất nên loại các phương án hàm bậc 3 và hàm phân thức bậc nhất chia bậc nhất.
Còn lại hai hàm Phân thức bậc hai chia bậc hai có cùng tiệm cận đứng và tiệm cận xiên nên sẽ lấy điểm thuộc đồ thị thay vào kiểm tra để phân biệt hai hàm số còn lại.

Phân tích và Phương pháp giải

Dạng bài toán yêu cầu nhận dạng đồ thị của hàm số phân thức bậc hai chia bậc nhất ($y = \frac{ax^2+bx+c}{dx+e}$) dựa trên các đặc điểm hình học của nó. Phương pháp giải chủ yếu bao gồm:
1. Xác định Tiệm cận đứng (VA): Đồ thị có VA tại nghiệm của mẫu số ($dx+e=0$). Trong bài toán gốc, VA là $x=0$.
2. Xác định Tiệm cận xiên (SA): Do bậc tử lớn hơn bậc mẫu 1 đơn vị, đồ thị có SA. SA được tìm bằng phép chia đa thức.
3. Kiểm tra các điểm đặc biệt: Nghiệm ($y=0$), giao điểm với trục Oy (nếu có), hoặc một điểm cụ thể mà đồ thị đi qua, để phân biệt giữa các hàm số có cùng tiệm cận.

Bài toán tương tự

Dưới đây là 5 bài toán tương tự:

**1.** Đồ thị dưới đây là của hàm số nào? (Giả sử đồ thị có Tiệm cận đứng $x=1$ và Tiệm cận xiên $y=x+1$, đi qua gốc tọa độ O(0; 0)).
**A.** $y=\frac{x^2}{x-1}$. **B.** $y=\frac{x^2+2x}{x-1}$.
**C.** $y=\frac{x^2+x+1}{x+1}$. **D.** $y=\frac{x^2+x}{x-2}$.
Đáp án đúng: **A.**
Lời giải ngắn gọn: Đồ thị có Tiệm cận đứng $x=1$, loại C, D. Hàm số đi qua O(0; 0) nên tử số phải bằng 0 khi $x=0$. Chỉ có $y=\frac{x^2}{x-1}$ thỏa mãn $y(0)=0$. Kiểm tra SA: $y=\frac{x^2}{x-1} = x + 1 + \frac{1}{x-1}$, SA là $y=x+1$.

**2.** Cho hàm số $y=f(x)$ có đồ thị như mô tả: Đồ thị có Tiệm cận đứng $x=-2$ và Tiệm cận xiên $y=2x+1$. Hàm số đi qua điểm $(-1; 0)$. Hàm số đó là:
**A.** $y=\frac{2x^2+5x+3}{x+2}$. **B.** $y=\frac{x^2+3x+2}{x+2}$.
**C.** $y=\frac{2x^2+x+2}{x+2}$. **D.** $y=\frac{2x^2-3x-5}{x-2}$.
Đáp án đúng: **A.**
Lời giải ngắn gọn: Đồ thị có Tiệm cận đứng $x=-2$, loại D. Đồ thị đi qua $(-1; 0)$, nghĩa là $-1$ là nghiệm của tử số. Kiểm tra A: $2(-1)^2 + 5(-1) + 3 = 2 – 5 + 3 = 0$ (Đúng). Kiểm tra SA của A: $y = \frac{2x(x+2) + x + 3}{x+2} = 2x + \frac{x+3}{x+2} = 2x + 1 + \frac{1}{x+2}$. SA là $y=2x+1$. (Đúng).

**3.** Nhận biết hàm số có đồ thị sau: Đồ thị có VA tại $x=-1$, SA có hệ số góc âm ($y=-x+k$). Đồ thị cắt trục Ox tại hai điểm phân biệt, trong đó có điểm $x=0$.
**A.** $y=\frac{x^2+x}{x+1}$. **B.** $y=\frac{-x^2+2x}{x+1}$.
**C.** $y=\frac{-x^2-x}{x-1}$. **D.** $y=\frac{-x^2+x}{x+1}$.
Đáp án đúng: **D.**
Lời giải ngắn gọn: VA tại $x=-1$, loại C. SA có hệ số góc âm, nên hệ số của $x^2$ ở tử và $x$ ở mẫu phải khác dấu (hoặc cùng dấu và phép chia cho ra kết quả âm). Kiểm tra D: $y=\frac{-x^2+x}{x+1} = -x + 2 – \frac{2}{x+1}$. SA là $y=-x+2$ (hệ số âm, thỏa mãn). Đồ thị cắt Ox tại $x=0$ và $x=1$ (vì $-x^2+x = 0$ khi $x=0, x=1$).

**4.** Đồ thị hàm số $y=\frac{x^2-4x+3}{x-2}$ có các tiệm cận là:
**A.** VA $x=2$, SA $y=x-2$. **B.** VA $x=2$, SA $y=x+2$.
**C.** VA $x=-2$, SA $y=x-2$. **D.** VA $x=2$, SA $y=x-4$.
Đáp án đúng: **A.**
Lời giải ngắn gọn: VA: Mẫu bằng 0 khi $x-2=0 \Rightarrow x=2$. SA: Thực hiện phép chia đa thức: $x^2-4x+3 = (x-2)(x-2) – 1$. Do đó $y = x-2 – \frac{1}{x-2}$. SA là $y=x-2$.

**5.** Cho đồ thị hàm số có VA $x=3$, SA $y=x-5$. Điểm cực trị nằm trên trục tung (giả sử $x_{CT}=0$). Hàm số phù hợp là:
**A.** $y=\frac{x^2+2x+1}{x-3}$. **B.** $y=\frac{x^2-5x}{x-3}$.
**C.** $y=\frac{x^2-8x+16}{x-3}$. **D.** $y=\frac{x^2-2x}{x+3}$.
Đáp án đúng: **C.**
Lời giải ngắn gọn: VA $x=3$, loại A, D. Kiểm tra SA của C: $y=\frac{x^2-8x+16}{x-3}$. Thực hiện phép chia: $x^2-8x+16 = (x-3)(x-5) + 1$. Vậy $y = x-5 + \frac{1}{x-3}$. SA là $y=x-5$. (Thỏa mãn. Lưu ý: Điều kiện về cực trị $x_{CT}=0$ thường phức tạp hơn, nhưng dựa vào VA và SA đã có thể loại trừ 3 phương án còn lại.)