Bài toán gốc
Cho hàm số $y=\dfrac{ax+b}{cx+d}$ có đồ thị như hình vẽ bên. Toạ độ giao điểm của đồ thị hàm số đã cho với trục tung là
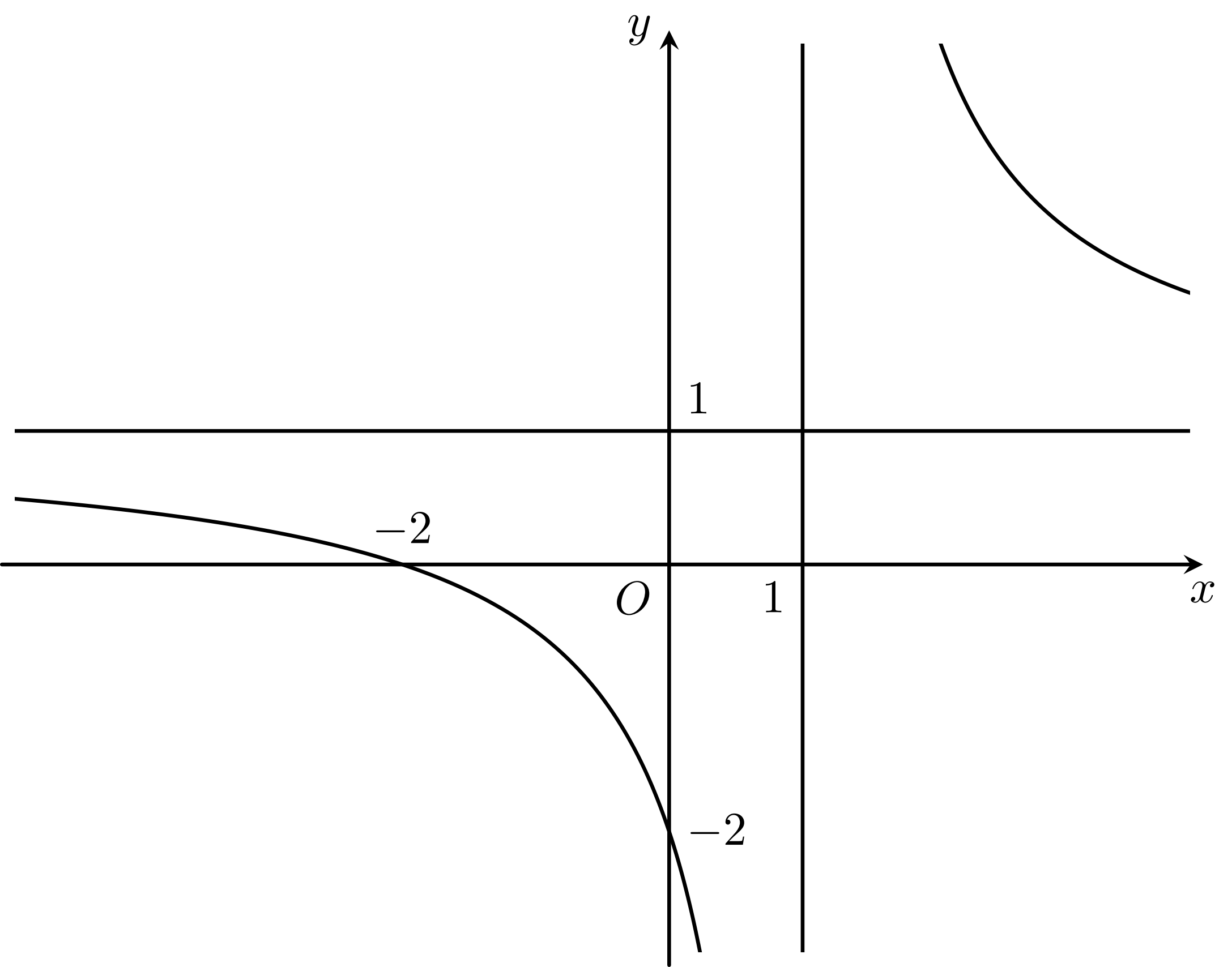
A. $(0;-2)$.B. $(-2;-2)$.C. $(-2;0)$.D. $(0;-2)$.
Lời giải: Từ đồ thị ta thấy giao điểm của đồ thị hàm số với trục tung có toạ độ là $(0;-2)$.
Phân tích và Phương pháp giải
Dạng bài toán yêu cầu nhận biết tọa độ giao điểm của đồ thị hàm số với trục tung ($Oy$) thông qua việc quan sát đồ thị. Phương pháp giải là đọc trực tiếp tọa độ của điểm mà đồ thị cắt trục $Oy$. Điểm này luôn có hoành độ bằng 0, tức là có dạng $(0; y_0)$.
Bài toán tương tự
5 bài toán tương tự:
**1. (Tương tự)** Cho hàm số $y=f(x)$ có đồ thị như hình vẽ bên. Tìm toạ độ giao điểm của đồ thị hàm số đã cho với trục tung.
(Hình minh họa: Đồ thị hàm số bất kỳ đi qua điểm $(0; 1)$ trên trục $Oy$).
A. $(1; 0)$.
B. $(0; 1)$.
C. $(1; 1)$.
D. $(-1; 0)$.
Đáp án đúng: B.
Lời giải ngắn gọn: Giao điểm với trục tung là điểm có hoành độ $x=0$. Quan sát đồ thị ta thấy nó cắt trục tung tại điểm có tung độ $y=1$. Vậy toạ độ giao điểm là $(0; 1)$.
**2. (Tương tự)** Đồ thị hàm số $y=f(x)$ được cho như hình vẽ sau. Toạ độ giao điểm của đồ thị hàm số này với trục $Oy$ là:
(Hình minh họa: Đồ thị hàm số cắt trục tung tại điểm $(0; -3)$).
A. $(-3; 0)$.
B. $(0; 3)$.
C. $(3; 0)$.
D. $(0; -3)$.
Đáp án đúng: D.
Lời giải ngắn gọn: Giao điểm với trục tung là điểm có hoành độ $x=0$. Dựa vào đồ thị, khi $x=0$, đồ thị đi qua điểm có tung độ $y=-3$. Vậy giao điểm là $(0; -3)$.
**3. (Tương tự)** Cho hàm số $y=f(x)$ có đồ thị là đường cong trong hình bên. Tìm toạ độ giao điểm của đồ thị hàm số với trục $Oy$.
(Hình minh họa: Đồ thị hàm số cắt trục tung tại điểm $(0; 2)$).
A. $(2; 0)$.
B. $(0; 2)$.
C. $(-2; 0)$.
D. $(0; -2)$.
Đáp án đúng: B.
Lời giải ngắn gọn: Giao điểm của đồ thị với trục tung là điểm có hoành độ $x=0$. Từ đồ thị, ta thấy khi $x=0$, $y=2$. Vậy giao điểm là $(0; 2)$.
**4. (Tương tự)** Cho hàm số $y=x^3-3x+3$ có đồ thị như hình vẽ. Giao điểm của đồ thị với trục tung có toạ độ là:
(Hình minh họa: Đồ thị hàm bậc ba cắt trục tung tại điểm $(0; 3)$).
A. $(3; 0)$.
B. $(-3; 0)$.
C. $(0; 3)$.
D. $(0; -3)$.
Đáp án đúng: C.
Lời giải ngắn gọn: Giao điểm với trục tung xảy ra khi $x=0$. Thay $x=0$ vào hàm số ta được $y(0) = 0^3 – 3(0) + 3 = 3$. Hoặc quan sát trực tiếp trên đồ thị, khi $x=0$, $y=3$. Toạ độ giao điểm là $(0; 3)$.
**5. (Tương tự)** Quan sát đồ thị hàm số $y=h(x)$ dưới đây. Hãy xác định toạ độ điểm mà đồ thị cắt trục tung.
(Hình minh họa: Đồ thị hàm số cắt trục tung tại điểm $(0; -1)$).
A. $(1; 0)$.
B. $(0; 1)$.
C. $(0; -1)$.
D. $(-1; 0)$.
Đáp án đúng: C.
Lời giải ngắn gọn: Giao điểm với trục tung là điểm nằm trên trục $Oy$, có hoành độ bằng 0. Dựa vào đồ thị, điểm đó có toạ độ $(0; -1)$.
