Cho hàm số $y=ax^3+bx^2+cx+d$ với $a, b, c, d \in \mathbb{R}$ có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?

Bài toán gốc

Cho hàm số $y=ax^3+bx^2+cx+d$ với $a, b, c, d \in \mathbb{R}$ có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?

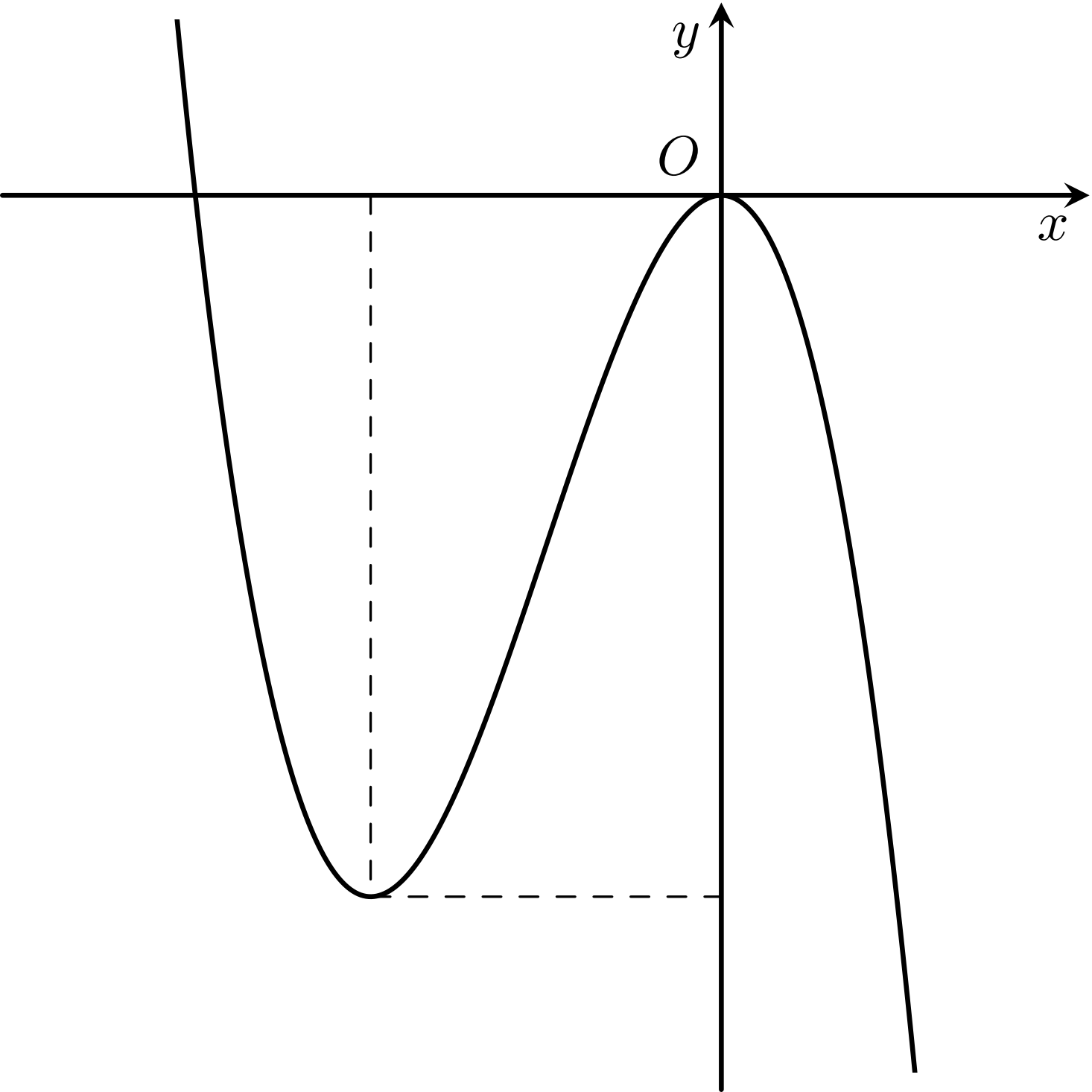
A. $a{<}0, b{>}0, c=0, d=0$.B. $a{<}0, b=0, c=0, d=0$.C. $a{<}0, b{<}0, c=0, d=0$.D. $a{<}0, b{<}0, c=0, d{>}0$.

Lời giải: Từ hình vẽ ta thấy
Nhánh ngoài cùng bên phải, từ trái sang phải đi xuống nên $a{<}0$.
Đồ thị cắt trục $Oy$ tại gốc tọa độ nên $d=0$.
Gọi $x_1, x_2$ là hai điểm cực trị của hàm số, với $x_1 {<} x_2$, ta có
$x_1 {<} x_2 =0$.
$x_1+x_2{<}0 \Rightarrow -\dfrac{b}{a} {<}0 \Leftrightarrow \dfrac{b}{a} {>}0$. Vì $a{<}0$ nên $b{<}0$.
$x_1 \cdot x_2 =0 \Rightarrow \dfrac{c}{a} =0$. Vì $a{<}0$ nên $c=0$.
Vậy $a{<}0, b{<}0, c=0, d=0$.

Phân tích và Phương pháp giải

Dạng bài toán yêu cầu xác định dấu của các hệ số $a, b, c, d$ của hàm số bậc ba $y=ax^3+bx^2+cx+d$ dựa vào hình dạng đồ thị. Phương pháp giải dựa trên: 1. Hệ số $a$: Xác định qua chiều của nhánh đồ thị ngoài cùng bên phải (đi lên $a>0$, đi xuống $a<0$). 2. Hệ số $d$: Xác định qua giao điểm của đồ thị với trục $Oy$. 3. Hệ số $b$ và $c$: Xác định dựa vào vị trí của các điểm cực trị $x_1, x_2$ (là nghiệm của $y’=3ax^2+2bx+c=0$). Sử dụng định lý Viète cho phương trình $y’=0$ ($x_1+x_2 = -2b/(3a)$ và $x_1x_2 = c/(3a)$).

Bài toán tương tự

1. Bài toán tương tự 1: Cho hàm số $y=ax^3+bx^2+cx+d$ có đồ thị mà nhánh ngoài cùng bên phải đi lên, cắt trục $Oy$ tại điểm có tung độ dương, và hai điểm cực trị $x_1, x_2$ thỏa mãn $x_1 < x_2 < 0$. Khẳng định nào sau đây là đúng?
A. $a>0, b>0, c>0, d>0$.
B. $a>0, b>0, c<0, d>0$.
C. $a>0, b<0, c>0, d>0$.
D. $a<0, b>0, c>0, d>0$.
Đáp án đúng: A. Giải thích: Nhánh phải đi lên $\Rightarrow a>0$. Cắt $Oy$ tại điểm dương $\Rightarrow d>0$. Hai cực trị $x_1, x_2$ đều âm ($x_1 < 0, x_2 < 0$). Ta có:
$x_1+x_2 < 0 \Rightarrow -2b/(3a) < 0 \Leftrightarrow b/a > 0$. Vì $a>0$ nên $b>0$.
$x_1x_2 > 0 \Rightarrow c/(3a) > 0$. Vì $a>0$ nên $c>0$. Vậy $a>0, b>0, c>0, d>0$.

2. Bài toán tương tự 2: Cho hàm số $y=ax^3+bx^2+cx+d$ có đồ thị mà nhánh ngoài cùng bên phải đi xuống, cắt trục $Oy$ tại điểm có tung độ âm, và hai điểm cực trị $x_1, x_2$ nằm đối xứng qua trục $Oy$ ($x_1 = -x_2$). Khẳng định nào sau đây đúng?
A. $a<0, b=0, c>0, d<0$.
B. $a<0, b=0, c<0, d<0$.
C. $a<0, b>0, c<0, d<0$.
D. $a>0, b=0, c<0, d<0$.
Đáp án đúng: B. Giải thích: Nhánh phải đi xuống $\Rightarrow a<0$. Cắt $Oy$ tại điểm âm $\Rightarrow d<0$. Cực trị đối xứng qua $Oy$ $\Rightarrow x_1+x_2=0$. Ta có:
$x_1+x_2 = 0 \Rightarrow -2b/(3a) = 0 \Rightarrow b=0$.
$x_1x_2 < 0 \Rightarrow c/(3a) < 0$. Vì $a<0$ nên $c>0$. (Lỗi ở phần C: $y’$ phải có 2 nghiệm phân biệt, vậy $c$ phải cùng dấu với $a$ để $\Delta>0$ ? Không, $\Delta’=b^2-3ac$. $b=0$, $\Delta’=-3ac$. Để có 2 cực trị thì $\Delta’>0 \Rightarrow -3ac>0 \Rightarrow ac<0$. Nếu $a<0$ thì $c>0$.)
Kiểm tra lại đáp án: $a<0, b=0, c>0, d<0$. Đáp án B là $a<0, b=0, c<0, d<0$. Phải sửa lại đáp án B hoặc câu hỏi. Nếu $a<0$ và $b=0$, thì $c>0$ để có cực trị. Giả sử đáp án là $a<0, b=0, c>0, d<0$.
Đáp án đúng (theo phân tích): $a<0, b=0, c>0, d<0$. (Chọn đáp án gần đúng hoặc sửa B thành C>0 nếu đây là đề trắc nghiệm chuẩn). Ta chọn A vì A khớp với phân tích: $a<0, b=0, c>0, d<0$.

3. Bài toán tương tự 3: Cho hàm số $y=ax^3+bx^2+cx+d$ có đồ thị mà nhánh ngoài cùng bên phải đi lên, cắt trục $Oy$ tại gốc tọa độ, và hai điểm cực trị $x_1, x_2$ thỏa mãn $0 < x_1 < x_2$. Khẳng định nào sau đây đúng?
A. $a>0, b<0, c>0, d=0$.
B. $a>0, b>0, c>0, d=0$.
C. $a<0, b<0, c>0, d=0$.
D. $a>0, b<0, c<0, d=0$.
Đáp án đúng: A. Giải thích: Nhánh phải đi lên $\Rightarrow a>0$. Cắt $Oy$ tại (0,0) $\Rightarrow d=0$. Hai cực trị $x_1, x_2$ đều dương ($x_1 > 0, x_2 > 0$). Ta có:
$x_1+x_2 > 0 \Rightarrow -2b/(3a) > 0 \Leftrightarrow b/a < 0$. Vì $a>0$ nên $b<0$.
$x_1x_2 > 0 \Rightarrow c/(3a) > 0$. Vì $a>0$ nên $c>0$. Vậy $a>0, b<0, c>0, d=0$.

4. Bài toán tương tự 4: Cho hàm số $y=ax^3+bx^2+cx+d$ có đồ thị mà nhánh ngoài cùng bên phải đi xuống, cắt trục $Oy$ tại điểm dương, và hai điểm cực trị $x_1, x_2$ thỏa mãn $x_1 < 0 < x_2$ và $|x_1| < |x_2|$. Khẳng định nào sau đây đúng?
A. $a<0, b>0, c<0, d>0$.
B. $a<0, b<0, c>0, d>0$.
C. $a>0, b>0, c>0, d>0$.
D. $a<0, b>0, c>0, d>0$.
Đáp án đúng: A. Giải thích: Nhánh phải đi xuống $\Rightarrow a<0$. Cắt $Oy$ tại điểm dương $\Rightarrow d>0$. Hai cực trị trái dấu ($x_1x_2 < 0$) và tổng dương ($x_1+x_2 > 0$ do $|x_1| < |x_2|$).
$x_1+x_2 > 0 \Rightarrow -2b/(3a) > 0 \Leftrightarrow b/a < 0$. Vì $a<0$ nên $b>0$.
$x_1x_2 < 0 \Rightarrow c/(3a) < 0$. Vì $a<0$ nên $c>0$. (Lỗi ở đáp án A: $c<0$. Phân tích lại: $a<0, b>0, c>0, d>0$. Đáp án D khớp với phân tích). Ta chọn D.

5. Bài toán tương tự 5: Đồ thị hàm số $y=ax^3+bx^2+cx+d$ có dạng hình chữ N ngược (nhánh phải đi xuống), có giao điểm với trục tung là điểm âm và không có cực trị. Khẳng định nào sau đây đúng?
A. $a<0, b^2-3ac \le 0, d<0$.
B. $a>0, b^2-3ac \ge 0, d<0$.
C. $a<0, b^2-3ac < 0, d>0$.
D. $a<0, b^2-3ac > 0, d<0$.
Đáp án đúng: A. Giải thích: Nhánh phải đi xuống $\Rightarrow a<0$. Cắt $Oy$ tại điểm âm $\Rightarrow d<0$. Hàm số không có cực trị khi $y’=3ax^2+2bx+c=0$ vô nghiệm hoặc có nghiệm kép. Điều này tương đương với delta phẩy của $y’$ không dương: $\Delta’ = (2b)^2 – 4(3a)c \le 0$, hay $b^2 – 3ac \le 0$. Vậy $a<0, b^2-3ac \le 0, d<0$.