Bài toán gốc
Cho hàm số $y=\dfrac{ax+b}{cx+d}$ với $ad-bc \ne 0$ và $c{<}0$ có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
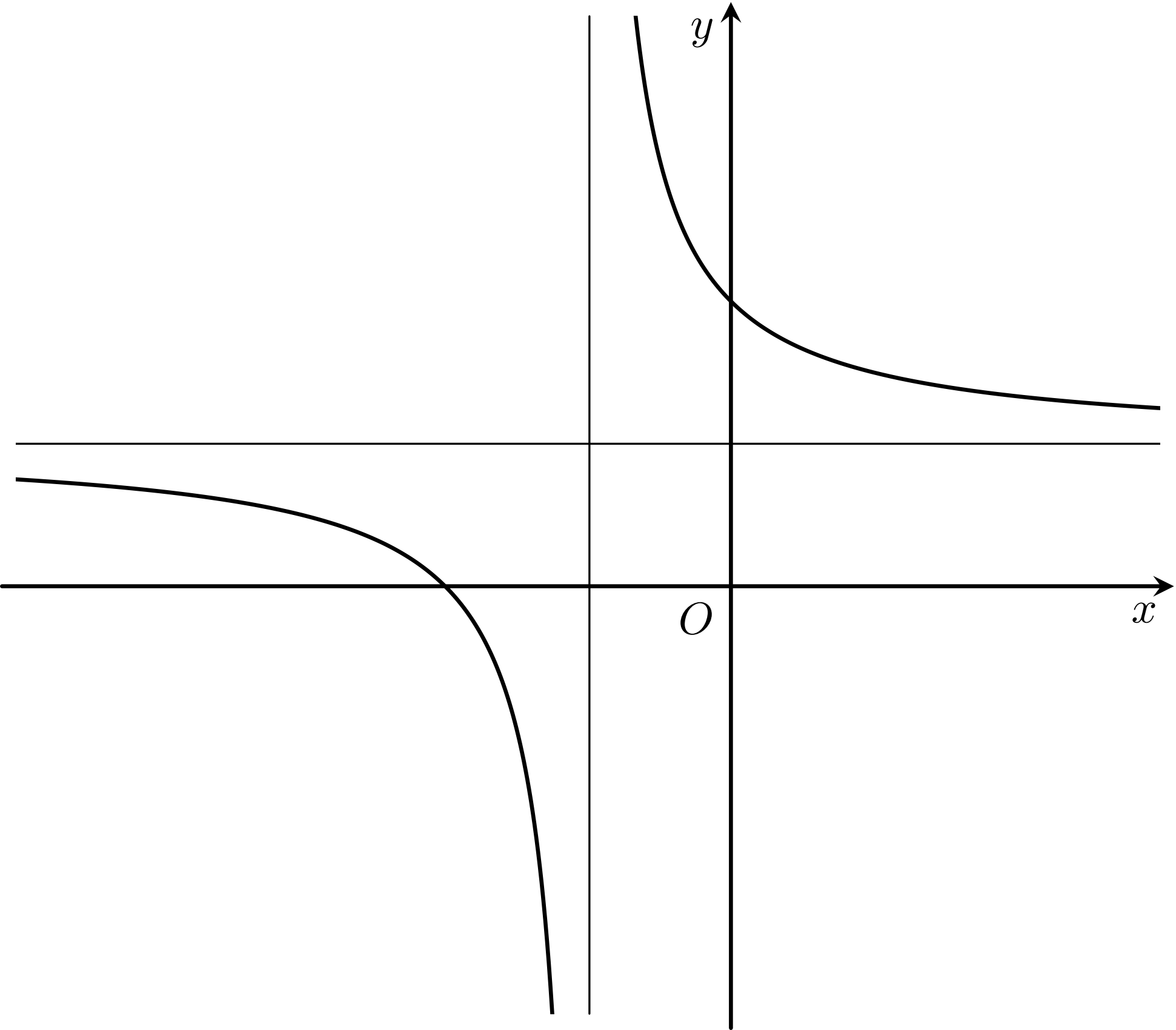
A. $a{<}0, b{<}0, d{<}0$.B. $a{<}0, b{<}0, d{>}0$.C. $a{>}0, b{<}0, d{>}0$.D. $a{>}0, b{>}0, d{<}0$.
Lời giải: Theo hàm số và đồ thị ta có
Tiệm cận ngang $y=\dfrac{a}{c}$ suy ra $\dfrac{a}{c}{>}0$, vì $c{<}0$ nên $a{<}0$.
Tiệm cận đứng $x=-\dfrac{d}{c}$ suy ra $-\dfrac{d}{c}{<}0 \Leftrightarrow \dfrac{d}{c}{>}0$, vì $c{<}0$ nên $d{<}0$.
Đồ thị cắt trục $Oy$ tại điểm có tung độ bằng $\dfrac{b}{d}$ suy ra $\dfrac{b}{d}{>}0$, vì $d{<}0$ nên $b{<}0$.
Vậy $a{>}0, b{<}0, d{<}0$.
Phân tích và Phương pháp giải
Dạng toán nhận biết dấu các hệ số $a, b, d$ (với $c$ thường được cố định dấu) của hàm phân thức $y=\dfrac{ax+b}{cx+d}$ dựa vào các đặc điểm hình học của đồ thị. Cần xác định vị trí của Tiệm cận ngang ($y=a/c$), Tiệm cận đứng ($x=-d/c$), và Giao điểm với trục tung ($y(0)=b/d)$ để suy ra dấu của các tỷ số tương ứng. Từ đó, kết hợp với điều kiện ràng buộc về dấu của $c$ (hoặc $d$) để tìm dấu của các hệ số còn lại.
Bài toán tương tự
Câu 1. Cho hàm số $y=\dfrac{ax+b}{cx+d}$ với $ad-bc \ne 0$ và $c{>}0$ có đồ thị như hình vẽ (Đồ thị tham chiếu: Tiệm cận ngang $y>0$, Tiệm cận đứng $x<0$, Giao $Oy$ tại $y>0$). Khẳng định nào sau đây đúng?
A. $a{>}0, b{>}0, d{<}0$. B. $a{<}0, b{>}0, d{<}0$. C. $a{>}0, b{>}0, d{>}0$. D. $a{<}0, b{<}0, d{>}0$.
Đáp án đúng: C.
Lời giải: TCN $y=a/c {>}0$. Vì $c{>}0$ nên $a{>}0$. TCĐ $x=-d/c {<}0 \Leftrightarrow d/c {>}0$. Vì $c{>}0$ nên $d{>}0$. Giao $Oy$: $y(0)=b/d {>}0$. Vì $d{>}0$ nên $b{>}0$. Vậy $a{>}0, b{>}0, d{>}0$.
Câu 2. Cho hàm số $y=\dfrac{ax+b}{cx+d}$ với $ad-bc \ne 0$ và $c{<}0$ có đồ thị có các đặc điểm: Tiệm cận ngang $y<0$, Tiệm cận đứng $x>0$, Giao điểm $Oy$ tại $y<0$. Khẳng định nào sau đây đúng?
A. $a{>}0, b{>}0, d{>}0$. B. $a{<}0, b{>}0, d{<}0$. C. $a{<}0, b{<}0, d{>}0$. D. $a{>}0, b{<}0, d{>}0$.
Đáp án đúng: D.
Lời giải: TCN $y=a/c {<}0$. Vì $c{<}0$ nên $a{>}0$. TCĐ $x=-d/c {>}0 \Leftrightarrow d/c {<}0$. Vì $c{<}0$ nên $d{>}0$. Giao $Oy$: $y(0)=b/d {<}0$. Vì $d{>}0$ nên $b{<}0$. Vậy $a{>}0, b{<}0, d{>}0$.
Câu 3. Cho hàm số $y=\dfrac{ax+b}{cx+d}$ có đồ thị có các đặc điểm: Tiệm cận ngang $y<0$, Tiệm cận đứng $x<0$, Giao điểm $Oy$ tại $y>0$. Mệnh đề nào sau đây là sai?
A. $a$ và $c$ cùng dấu. B. $b$ và $d$ cùng dấu. C. $a$ và $d$ cùng dấu. D. $a$ và $b$ cùng dấu.
Đáp án đúng: C.
Lời giải: TCN $a/c {<}0$ nên $a, c$ trái dấu. TCĐ $-d/c {<}0 \Leftrightarrow d/c {>}0$ nên $d, c$ cùng dấu. Giao $Oy$: $b/d {>}0$ nên $b, d$ cùng dấu. Từ đó suy ra $a$ và $d$ luôn trái dấu, và $a$ và $b$ luôn trái dấu.
A. $a, c$ trái dấu (Đúng). B. $b, d$ cùng dấu (Đúng). C. $a, d$ cùng dấu (SAI). D. $a, b$ trái dấu (Đúng).
Vậy khẳng định SAI là C.
Câu 4. Cho hàm số $y=\dfrac{ax+b}{cx+d}$ với $ad-bc \ne 0$ và $c{>}0$ có đồ thị đi qua gốc tọa độ $O(0; 0)$. Đồ thị có Tiệm cận ngang $y<0$ và Tiệm cận đứng $x<0$. Mệnh đề nào sau đây đúng?
A. $a{>}0, d{<}0$. B. $a{<}0, d{<}0$. C. $a{<}0, d{>}0$. D. $a{>}0, d{>}0$.
Đáp án đúng: C.
Lời giải: Đồ thị đi qua $O(0; 0)$ nên $y(0)=b/d=0$, suy ra $b=0$. TCN $y=a/c {<}0$. Vì $c{>}0$ nên $a{<}0$. TCĐ $x=-d/c {<}0 \Leftrightarrow d/c {>}0$. Vì $c{>}0$ nên $d{>}0$. Vậy $a{<}0, d{>}0$.
Câu 5. Cho hàm số $y=\dfrac{x+m}{nx+p}$ có đồ thị có Tiệm cận ngang $y<0$, Tiệm cận đứng $x>0$, Giao $Oy$ tại $y<0$. Biết $n{<}0$. Khẳng định nào sau đây đúng về dấu của $m$ và $p$?
A. $m{>}0, p{>}0$. B. $m{<}0, p{>}0$. C. $m{>}0, p{<}0$. D. $m{<}0, p{<}0$.
Đáp án đúng: B.
Lời giải: Hàm số là $y=\dfrac{1x+m}{nx+p}$ (với $a=1, c=n$). Ta có $n{<}0$. TCN $y=1/n {<}0$ (Khớp với đồ thị). TCĐ $x=-p/n {>}0 \Leftrightarrow p/n {<}0$. Vì $n{<}0$ nên $p{>}0$. Giao $Oy$: $y(0)=m/p {<}0$. Vì $p{>}0$ nên $m{<}0$. Vậy $m{<}0, p{>}0$.
