Hàm số nào dưới đây có bảng biến thiên như sau?

Bài toán gốc

Hàm số nào dưới đây có bảng biến thiên như sau?

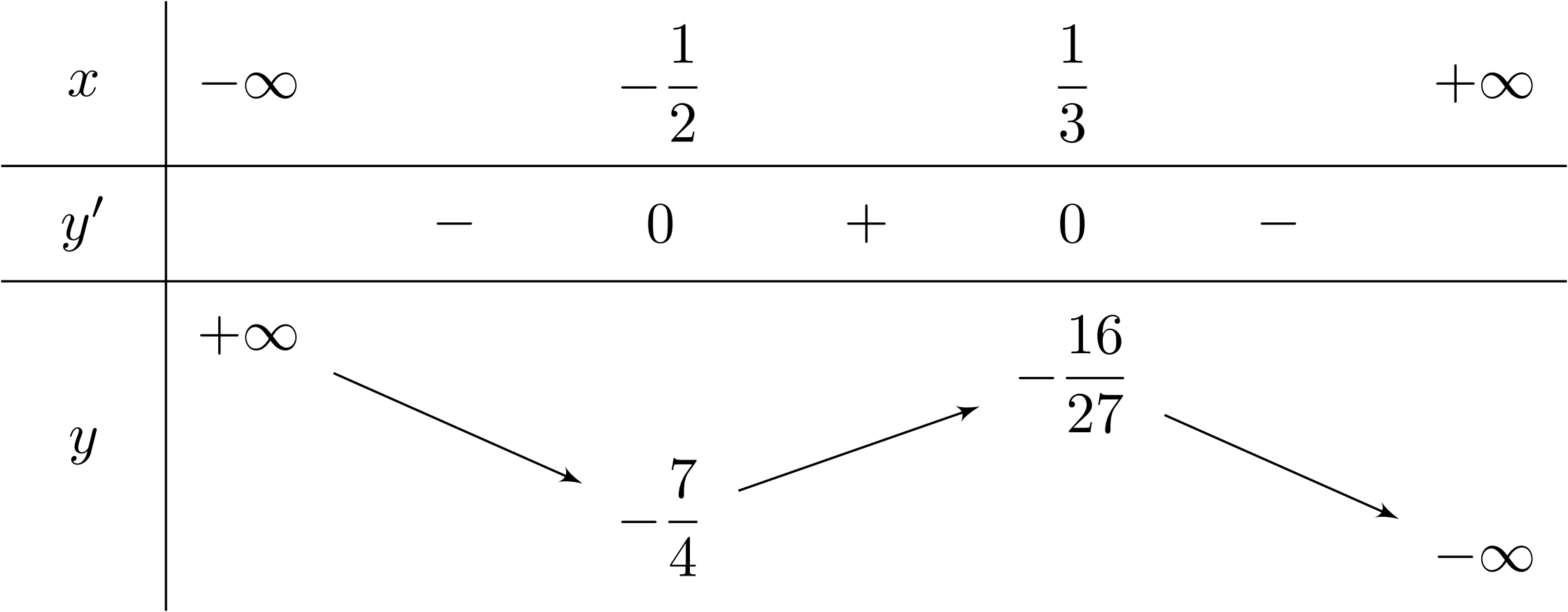
A. $y=\dfrac{-4x + 4}{x + 4}$.B. $y=-4x^3+x^2+2x-1$.

C. $y=-4x^2+x-1$.D. $y=-4x^4+x^2-1$.

Lời giải: Nhìn vào BBT ta thấy đạo hàm $y^{\prime} = 0$ có hai nghiệm $x_1=-\dfrac{1}{2}; x_2=\dfrac{1}{3}$ và hệ số $a = -4{<}0$.
Do đó BBT trên là của đồ thị hàm số $y=-4x^3+x^2+2x-1$.endvabi

Phân tích và Phương pháp giải

Dạng bài toán nhận biết hàm số dựa vào bảng biến thiên (BBT). Phương pháp giải là dựa vào các đặc điểm quan trọng của BBT:

1. Xác định bậc của hàm số (Cubic, Quartic, hoặc Rational) dựa trên số lượng cực trị (nghiệm của y’) và giới hạn khi x tiến tới vô cực.

2. Xác định dấu của hệ số bậc cao nhất (a) dựa trên xu hướng của hàm số khi x tiến tới +∞ (nếu a>0, y → +∞; nếu a<0, y → -∞).

3. Xác định các điểm cực trị hoặc tiệm cận (đối với hàm phân thức) để kiểm tra đạo hàm y’ hoặc các hằng số trong công thức hàm số.

Bài toán tương tự

1. Hàm số nào dưới đây có bảng biến thiên như sau?

BBT mô tả: x | -∞ 0 2 +∞; y’ | + 0 – 0 +; y | -∞ ↗ y(0) ↘ y(2) ↗ +∞

A. $y=x^3-3x^2+5$. B. $y=-x^3+3x^2+5$. C. $y=x^4-2x^2+5$. D. $y=\dfrac{2x+1}{x-1}$.

Đáp án đúng: A.

Lời giải ngắn gọn: BBT là của hàm bậc ba có hệ số $a>0$ (vì $\lim_{x \to +\infty} y = +\infty$) và có hai điểm cực trị tại $x=0$ và $x=2$. Hàm A: $y’ = 3x^2 – 6x = 3x(x-2)$. $y’=0 \Leftrightarrow x=0$ hoặc $x=2$. Thỏa mãn BBT.

2. Hàm số nào dưới đây có bảng biến thiên thể hiện hàm số đồng biến trên các khoảng xác định, có tiệm cận đứng $x=1$ và tiệm cận ngang $y=2$.

BBT mô tả: x | -∞ 1 +∞; y’ | + || +; y | 2 ↗ +∞ || -∞ ↗ 2

A. $y=\dfrac{2x+1}{x+1}$. B. $y=\dfrac{2x+3}{x-1}$. C. $y=\dfrac{x+2}{2x-2}$. D. $y=\dfrac{-2x+1}{x-1}$.

Đáp án đúng: D.

Lời giải ngắn gọn: Hàm phân thức $y=\dfrac{ax+b}{cx+d}$ có TCD $x=-d/c=1$ và TCN $y=a/c=2$. Loại A, C. Kiểm tra dấu đạo hàm. Hàm D: $y=\dfrac{-2x+1}{x-1}$. $y’ = \dfrac{(-2)(-1) – 1(1)}{(x-1)^2} = \dfrac{1}{(x-1)^2} > 0$. Hàm đồng biến. Thỏa mãn.

3. Hàm số nào dưới đây có bảng biến thiên như sau?

BBT mô tả: x | -∞ -1 0 1 +∞; y’ | + 0 – 0 + 0 -; y | -∞ ↗ y(-1) ↘ y(0) ↗ y(1) ↘ -∞

A. $y=x^4-2x^2+3$. B. $y=-x^4+2x^2+3$. C. $y=x^3-x$. D. $y=\dfrac{x}{x^2+1}$.

Đáp án đúng: B.

Lời giải ngắn gọn: BBT là của hàm bậc bốn trùng phương, hệ số $a<0$ (vì $\lim_{x \to \pm\infty} y = -\infty$) và có 3 cực trị tại $x=-1, 0, 1$. Hàm B: $y’ = -4x^3 + 4x = -4x(x^2 – 1)$. $y’=0$ tại $x=-1, 0, 1$. Thỏa mãn dấu của $y’$ trên các khoảng tương ứng.

4. Hàm số nào dưới đây có bảng biến thiên thể hiện hàm số luôn nghịch biến trên $\mathbb{R}$ và $\lim_{x \to +\infty} y = -\infty$.

BBT mô tả: x | -∞ +∞; y’ | -; y | +∞ ↘ -∞

A. $y=x^3+2x+1$. B. $y=-x^3+x^2-x+1$. C. $y=\dfrac{-2x+1}{x-1}$. D. $y=x^4+x^2+1$.

Đáp án đúng: B.

Lời giải ngắn gọn: Hàm số phải là hàm bậc ba với $a<0$ và không có cực trị. Hàm B: $y=-x^3+x^2-x+1$. Đạo hàm $y’ = -3x^2 + 2x – 1$. Ta có $\Delta’ = 1^2 – (-3)(-1) = -2 < 0$. Vì $a_{y'} = -3 < 0$ và $\Delta' < 0$, nên $y' < 0$ với mọi $x$. Hàm luôn nghịch biến trên $\mathbb{R}$.

5. Hàm số nào dưới đây có bảng biến thiên thể hiện hàm số nghịch biến trên các khoảng xác định, có tiệm cận đứng $x=-2$ và tiệm cận ngang $y=3$.

BBT mô tả: x | -∞ -2 +∞; y’ | – || -; y | 3 ↘ -∞ || +∞ ↘ 3

A. $y=\dfrac{3x+5}{x-2}$. B. $y=\dfrac{3x+1}{x+2}$. C. $y=\dfrac{3x-5}{x+2}$. D. $y=\dfrac{-3x+1}{x+2}$.

Đáp án đúng: D.

Lời giải ngắn gọn: TCD $x=-2$, TCN $y=3$. Chỉ B, C, D thỏa mãn tiệm cận. Hàm số nghịch biến nên $y’ < 0$. Xét D: $y=\dfrac{-3x+1}{x+2}$. $y' = \dfrac{(-3)(2) - 1(1)}{(x+2)^2} = \dfrac{-7}{(x+2)^2} < 0$. Hàm nghịch biến. Thỏa mãn.