Bài toán gốc
Đồ thị dưới đây là của hàm số nào?
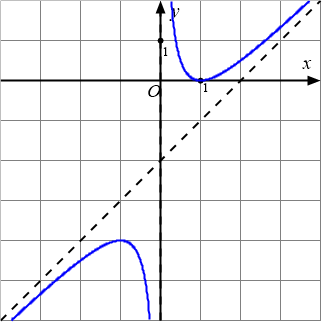
A. $y=\dfrac{x+2}{x-2}$.B. $y=\dfrac{x^2-2x+1}{x}$.
C. $y=-x^3+2x^2+x-3$.D. $y=\dfrac{x^2+2x+2}{-x-1}$.
Lời giải: Đây là dạng của đồ thị hàm bậc hai chia bậc nhất nên loại các phương án hàm bậc 3 và hàm phân thức bậc nhất chia bậc nhất.
Còn lại hai hàm Phân thức bậc hai chia bậc hai, kiểm tra tiệm cận đứng và tiệm cận xiên để loại trừ, nếu chưa được sẽ lấy điểm thuộc đồ thị thay vào kiểm tra để phân biệt hai hàm số còn lại.
Phân tích và Phương pháp giải
Dạng bài toán là nhận dạng đồ thị hàm số, cụ thể là hàm phân thức hữu tỉ $y = P(x)/Q(x)$. Đồ thị trong bài toán gốc có dạng hai nhánh cong, có một tiệm cận đứng (VA) và một tiệm cận xiên (SA), đây là đặc điểm của hàm số phân thức bậc hai chia bậc nhất ($y = (ax^2+bx+c)/(dx+e)$). Phương pháp giải bao gồm: (1) Loại trừ các hàm không phải phân thức bậc 2/bậc 1 (ví dụ: hàm bậc 3, hàm bậc 1/bậc 1). (2) Xác định Tiệm cận đứng (VA: nghiệm mẫu số) và Tiệm cận xiên (SA: chia đa thức). (3) Dùng các điểm đặc biệt (giao điểm với trục tọa độ) để chọn đáp án chính xác.
Bài toán tương tự
Sau đây là 5 bài toán tương tự về nhận dạng đồ thị hàm số:
1. Đồ thị trong hình vẽ là của hàm số nào?

A. $y = x^3 – 3x + 1$.
B. $y = \dfrac{x^2 – x}{x+1}$.
C. $y = \dfrac{2x+1}{x+1}$.
D. $y = \dfrac{x^2+1}{x-1}$.
Đáp án đúng: B.
Giải thích: Đồ thị có dạng hàm bậc 2/bậc 1. Tiệm cận đứng là $x = -1$. Tiệm cận xiên (thực hiện phép chia đa thức) là $y = x – 2$. (Hàm B: $y = \dfrac{x(x-1)}{x+1} = x – 2 + \dfrac{2}{x+1}$. VA: $x=-1$, SA: $y=x-2$).
2. Đồ thị dưới đây là của hàm số nào?

A. $y = \dfrac{x^2 – x + 1}{x+1}$.
B. $y = -x^4 + 2x^2 + 1$.
C. $y = \dfrac{-x^2 + 3x – 1}{x-2}$.
D. $y = \dfrac{x+1}{x-2}$.
Đáp án đúng: C.
Giải thích: Đồ thị có VA tại $x=2$ và SA có hệ số góc âm. Hàm C: $y = \dfrac{-x^2 + 3x – 1}{x-2}$. VA: $x=2$. Chia đa thức ta được $y = -x + 1 + \dfrac{1}{x-2}$. Vậy SA là $y=-x+1$ (hệ số góc âm). Đồ thị đi qua điểm $(0; 1/2)$, thỏa mãn.
3. Hàm số nào sau đây có đồ thị như hình vẽ?

A. $y = x^3 – 3x$.
B. $y = \dfrac{x^2}{x-1}$.
C. $y = \dfrac{2x-1}{x-1}$.
D. $y = \dfrac{x^2+x-1}{x+2}$.
Đáp án đúng: B.
Giải thích: Đồ thị có VA $x=1$ và SA có hệ số góc dương ($y=x+1$). Hàm B: $y = \dfrac{x^2}{x-1} = x + 1 + \dfrac{1}{x-1}$. VA: $x=1$. SA: $y=x+1$.
4. Cho hàm số $y=f(x)$ có đồ thị như hình bên. Hỏi đó là hàm số nào trong các hàm số dưới đây?

A. $y = \dfrac{x^2+x-1}{x+2}$.
B. $y = -x^3+x-1$.
C. $y = \dfrac{-x^2-x+1}{x+2}$.
D. $y = \dfrac{x+1}{x+2}$.
Đáp án đúng: C.
Giải thích: Đồ thị có VA $x=-2$ và SA có hệ số góc âm. Hàm C: $y = \dfrac{-x^2-x+1}{x+2}$. VA: $x=-2$. Chia đa thức ta được $y = -x + 1 – \dfrac{1}{x+2}$. SA: $y=-x+1$. Thỏa mãn.
5. Đồ thị dưới đây là của hàm số nào?

A. $y = \dfrac{x^2 – x + 1}{x-1}$.
B. $y = \dfrac{x^2+1}{x}$.
C. $y = x^4 – 2x^2 + 3$.
D. $y = \dfrac{x+1}{x}$.
Đáp án đúng: B.
Giải thích: Đồ thị có VA $x=0$ (trục tung) và SA có hệ số góc dương. Hàm B: $y = \dfrac{x^2+1}{x} = x + \dfrac{1}{x}$. VA: $x=0$. SA: $y=x$.
