Bài toán gốc
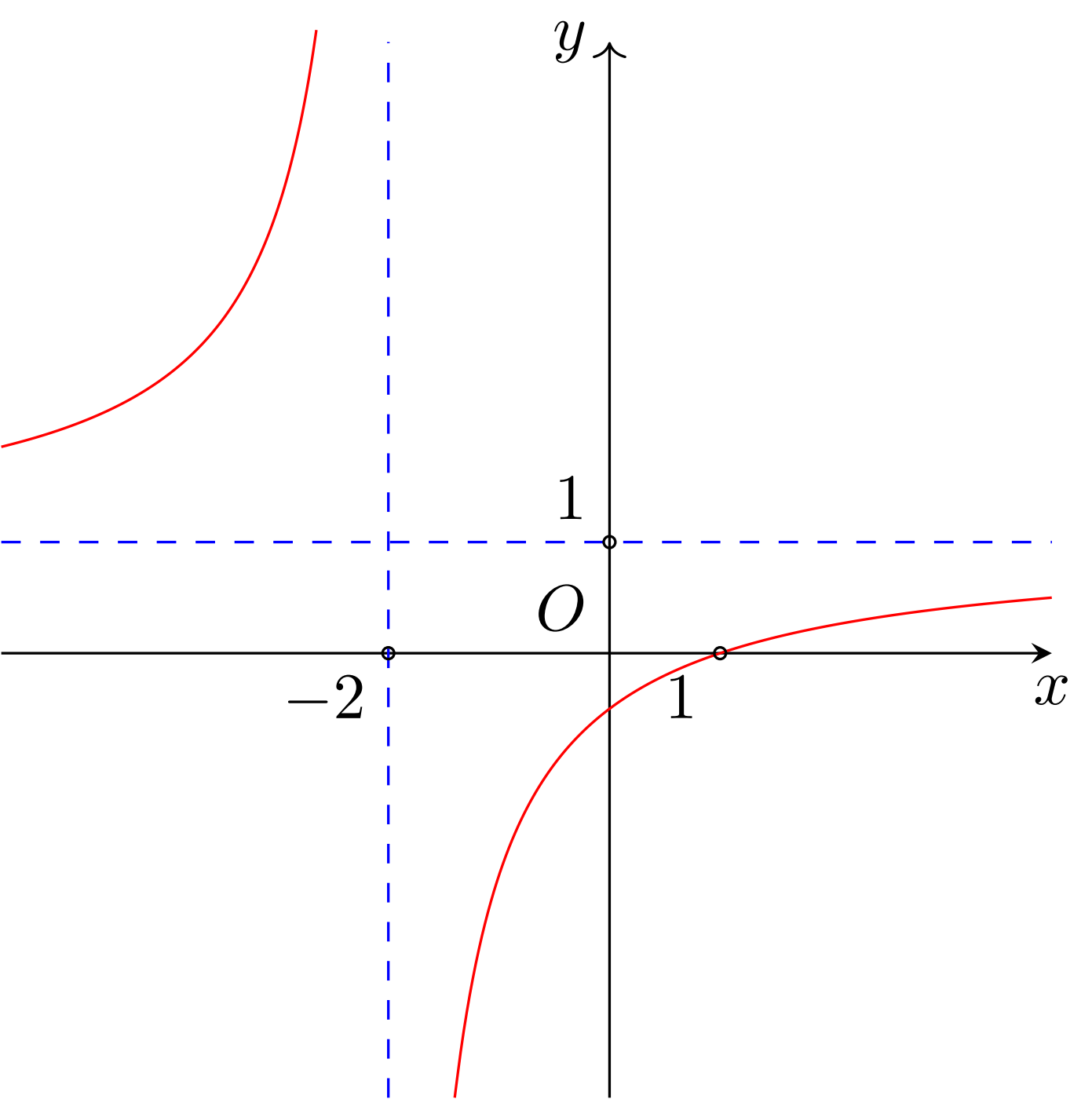
Cho hàm số có đồ thị như hình vẽ bên dưới. Số giao điểm của đồ thị với trục tung là
A. $2$.B. $0$.C. $3$.D. $1$.
Lời giải: Nhìn vào đồ thị ta thấy đồ thị hàm số cắt trục tung tại một điểm.
Phân tích và Phương pháp giải
Dạng toán này yêu cầu học sinh nhận biết và đọc các đặc điểm cơ bản của đồ thị hàm số, cụ thể là xác định số lượng giao điểm của đồ thị với các trục tọa độ. Trục tung là đường thẳng $x=0$. Vì $y=f(x)$ là một hàm số (với mỗi $x$ chỉ có tối đa một giá trị $y$), nên đồ thị hàm số luôn cắt trục tung tại tối đa một điểm (chỉ cắt 1 lần nếu hàm số xác định tại $x=0$, và không cắt nếu hàm số không xác định tại $x=0$). Phương pháp giải là quan sát trực tiếp đồ thị để đếm số lần đường cong cắt trục Oy.
Bài toán tương tự
Câu 1. Cho hàm số $y=f(x)$ có đồ thị là một đường cong trơn (như đồ thị của hàm đa thức bậc ba) và cắt trục hoành tại ba điểm phân biệt. Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu điểm chung với trục tọa độ Oy?
A. $3$.
B. $1$.
C. $0$.
D. $2$.
Đáp án đúng: B. Lời giải ngắn gọn: Đồ thị của hàm số $y=f(x)$ (hàm số thông thường) luôn cắt trục tung Oy ($x=0$) tại duy nhất một điểm (giả sử hàm số xác định tại $x=0$), độc lập với số giao điểm với trục Ox.
Câu 2. Cho hàm số $y = x^4 – 2x^2 + 1$. Số giao điểm của đồ thị hàm số này với trục tung là:
A. $4$.
B. $2$.
C. $1$.
D. $0$.
Đáp án đúng: C. Lời giải ngắn gọn: Giao điểm với trục tung là điểm có hoành độ $x=0$. Thay $x=0$ vào hàm số, ta được $y = 0^4 – 2(0)^2 + 1 = 1$. Đồ thị cắt trục tung tại duy nhất điểm $(0; 1)$.
Câu 3. Cho đồ thị hàm số $y=f(x)$ như hình vẽ, biết đồ thị có tiệm cận ngang $y=2$ và tiệm cận đứng $x=-1$. Đồ thị hàm số này có bao nhiêu điểm chung với trục hoành?
A. $1$.
B. $0$.
C. $2$.
D. $3$.
Đáp án đúng: A. Lời giải ngắn gọn: Để tìm giao điểm với trục hoành ($y=0$), ta xét phương trình $f(x)=0$. Dựa trên hình vẽ điển hình của hàm phân thức $y=(ax+b)/(cx+d)$ với tiệm cận ngang $y=2$, nếu đồ thị cắt trục hoành thì nó chỉ cắt tại một điểm duy nhất (tức là phương trình $f(x)=0$ có 1 nghiệm duy nhất).
Câu 4. Cho hàm số $y=f(x)$ có đồ thị như hình vẽ. Nếu đồ thị đi qua gốc tọa độ $O(0; 0)$ và cắt trục hoành thêm một lần nữa tại điểm có hoành độ dương, thì đồ thị này có bao nhiêu giao điểm với trục tung?
A. $0$.
B. $1$.
C. $2$.
D. $3$.
Đáp án đúng: B. Lời giải ngắn gọn: Việc đồ thị cắt trục hoành bao nhiêu lần không ảnh hưởng đến số giao điểm với trục tung. Vì đồ thị đi qua gốc tọa độ $O(0; 0)$, điểm này vừa là giao điểm với trục hoành vừa là giao điểm với trục tung. Vì là hàm số, tại $x=0$ chỉ có một giá trị $y=0$, nên đồ thị chỉ có 1 giao điểm với trục tung.
Câu 5. Cho hàm số $y=f(x)$ có đồ thị đi qua điểm $A(0; -5)$. Số giao điểm của đồ thị hàm số đã cho với trục tung là:
A. Lớn hơn 1.
B. $0$.
C. $1$.
D. $2$.
Đáp án đúng: C. Lời giải ngắn gọn: Điểm $A(0; -5)$ là điểm có hoành độ $x=0$, tức là giao điểm của đồ thị với trục tung. Vì $y=f(x)$ là hàm số, chỉ có duy nhất một giá trị $y$ tại $x=0$. Vậy đồ thị chỉ có 1 giao điểm với trục tung.
