Cho hàm số $y=\dfrac{ax+b}{6x+d}$ có đồ thị như hình vẽ bên. Giá trị biểu thức $T=8a+8b-d$ bằng

Bài toán gốc

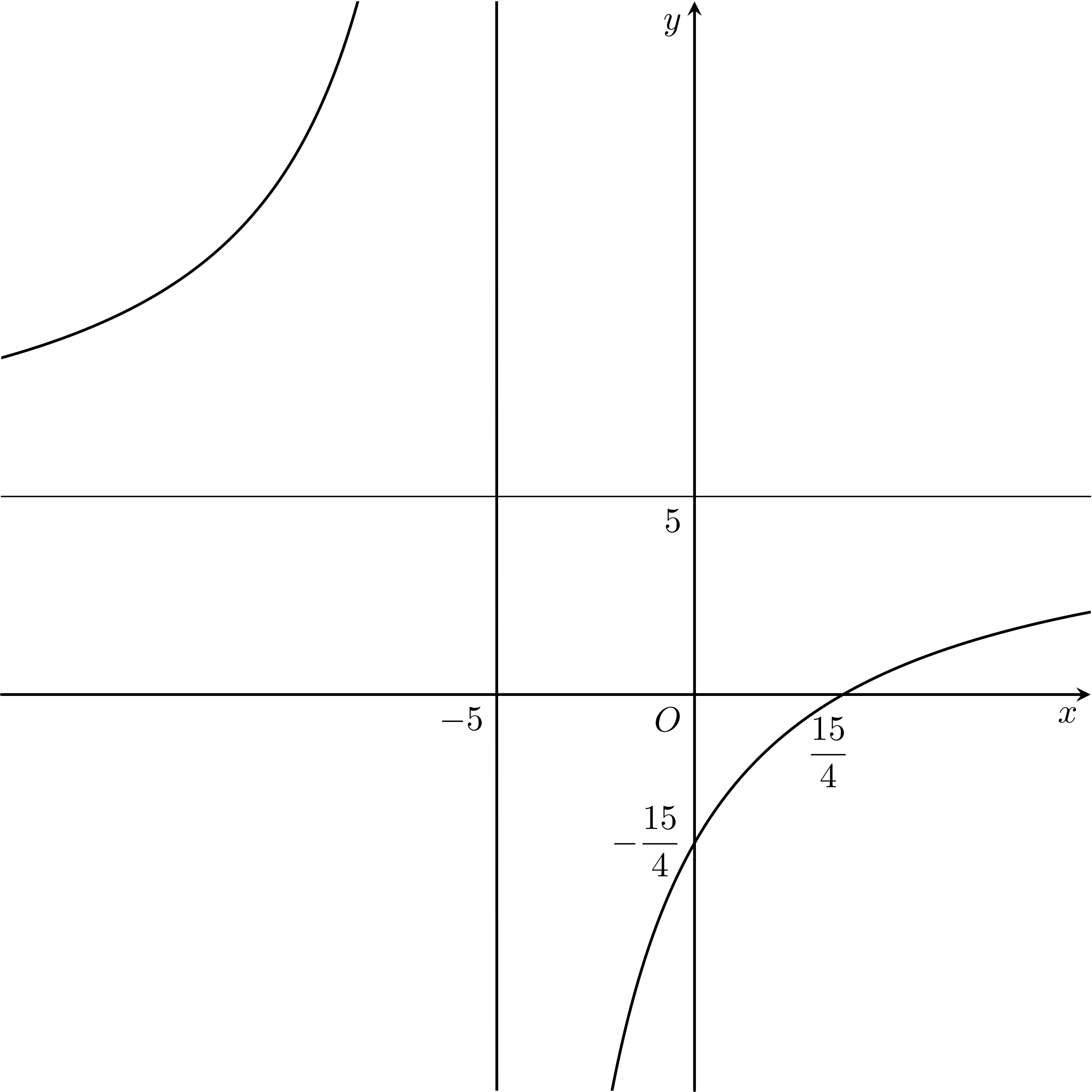
Cho hàm số $y=\dfrac{ax+b}{6x+d}$ có đồ thị như hình vẽ bên. Giá trị biểu thức $T=8a+8b-d$ bằng

A. $-692$.B. $-690$.C. $-693$.D. $-689$.

Lời giải: Dựa vào hàm số và đồ thị ta có
Tiệm cận ngang $y=\dfrac{a}{6}\Rightarrow\dfrac{a}{6}= 5 \Leftrightarrow a=30$.{1 cm}$(1)$
Giao trục $Ox$ tại điểm có hoành độ $x_0=\dfrac{-b}{a} \Rightarrow \dfrac{-b}{a}=\dfrac{15}{4}\Leftrightarrow b=- \dfrac{15}{4}\cdot 30\Leftrightarrow b=- \dfrac{225}{2}$.{1 cm} $(2)$
Tiệm cận đứng $x=\dfrac{-d}{6} \Rightarrow \dfrac{-d}{6}=-5\Leftrightarrow d=30$.{1 cm}$(3)$
Thay $(1);(2);(3)$ vào $T$ ta được $T=8\cdot30+8\cdot\left(- \dfrac{225}{2}\right)-1\cdot30=-690$.

Phân tích và Phương pháp giải

Dạng toán nhận dạng hàm số phân thức bậc nhất trên bậc nhất $y=\dfrac{Ax+B}{Cx+D}$ thông qua đồ thị. Phương pháp giải là xác định các tham số $A, B, C, D$ (hoặc $a, b, d$ trong đề bài gốc với $C=6$) dựa trên ba đặc điểm cơ bản của đồ thị: 1) Tiệm cận ngang (TCN): $y=A/C$; 2) Tiệm cận đứng (TCĐ): $x=-D/C$; 3) Giao điểm với trục tọa độ (Giao Ox: $x=-B/A$, Giao Oy: $y=B/D$). Sau khi xác định được các tham số, thay chúng vào biểu thức $T$ cần tính.

Bài toán tương tự

5 bài toán tương tự:

**1.** Cho hàm số $y=\dfrac{ax+b}{2x+d}$. Biết đồ thị hàm số có tiệm cận đứng $x=1$, tiệm cận ngang $y=3$ và đi qua điểm $(-1/2, 0)$. Giá trị biểu thức $T=a+b+d$ bằng:
A. 9. B. 7. C. 5. D. 3.
Đáp án đúng: B.
Lời giải ngắn gọn: TCN $y=a/2 = 3 \Rightarrow a=6$. TCĐ $x=-d/2 = 1 \Rightarrow d=-2$. Điểm $(-1/2, 0)$ là giao Ox: $-b/a = -1/2 \Rightarrow b=a/2=3$. Thay vào $T$: $T = 6+3+(-2) = 7$.

**2.** Cho hàm số $y=\dfrac{ax+b}{x+d}$. Biết đồ thị hàm số có tiệm cận đứng $x=-3$, tiệm cận ngang $y=2$ và cắt trục $Oy$ tại $y=1$. Giá trị biểu thức $T=5a-2b+d$ bằng:
A. 7. B. 9. C. 11. D. 13.
Đáp án đúng: A.
Lời giải ngắn gọn: TCN $y=a/1 = 2 \Rightarrow a=2$. TCĐ $x=-d/1 = -3 \Rightarrow d=3$. Giao Oy $y=b/d = 1 \Rightarrow b=d=3$. $T = 5(2) – 2(3) + 3 = 10 – 6 + 3 = 7$.

**3.** Cho hàm số $y=\dfrac{ax+b}{3x+d}$. Biết đồ thị hàm số có tiệm cận ngang $y=-1$, tiệm cận đứng $x=2$ và cắt trục hoành tại $x=1$. Tính giá trị của $T=a+2b+d$.
A. 1. B. -1. C. -3. D. 3.
Đáp án đúng: C.
Lời giải ngắn gọn: TCN $y=a/3 = -1 \Rightarrow a=-3$. TCĐ $x=-d/3 = 2 \Rightarrow d=-6$. Giao Ox $x=-b/a = 1 \Rightarrow b=-a=3$. $T = -3 + 2(3) + (-6) = -3$.

**4.** Cho hàm số $y=\dfrac{ax+b}{4x+d}$. Biết đồ thị có TCĐ $x=1/2$, TCN $y=1/4$ và đi qua điểm $(0, -1/4)$. Giá trị biểu thức $T=4a+2b+5d$ bằng:
A. -5. B. 0. C. 5. D. -10.
Đáp án đúng: A.
Lời giải ngắn gọn: TCN $y=a/4 = 1/4 \Rightarrow a=1$. TCĐ $x=-d/4 = 1/2 \Rightarrow d=-2$. Giao Oy $y=b/d = -1/4 \Rightarrow b/(-2) = -1/4 \Rightarrow b=1/2$. $T = 4(1) + 2(1/2) + 5(-2) = 4 + 1 – 10 = -5$.

**5.** Cho hàm số $y=\dfrac{ax+b}{x+d}$. Biết đồ thị hàm số có TCĐ $x=1/3$, TCN $y=-3$ và cắt trục hoành tại $x=-2$. Giá trị biểu thức $T=3a+3b+9d$ bằng:
A. -27. B. -30. C. 0. D. 30.
Đáp án đúng: B.
Lời giải ngắn gọn: TCN $y=a/1 = -3 \Rightarrow a=-3$. TCĐ $x=-d/1 = 1/3 \Rightarrow d=-1/3$. Giao Ox $x=-b/a = -2 \Rightarrow b=2a=-6$. $T = 3(-3) + 3(-6) + 9(-1/3) = -9 – 18 – 3 = -30.