Hàm số nào có bảng biến thiên như sau?

Bài toán gốc

Hàm số nào có bảng biến thiên như sau?

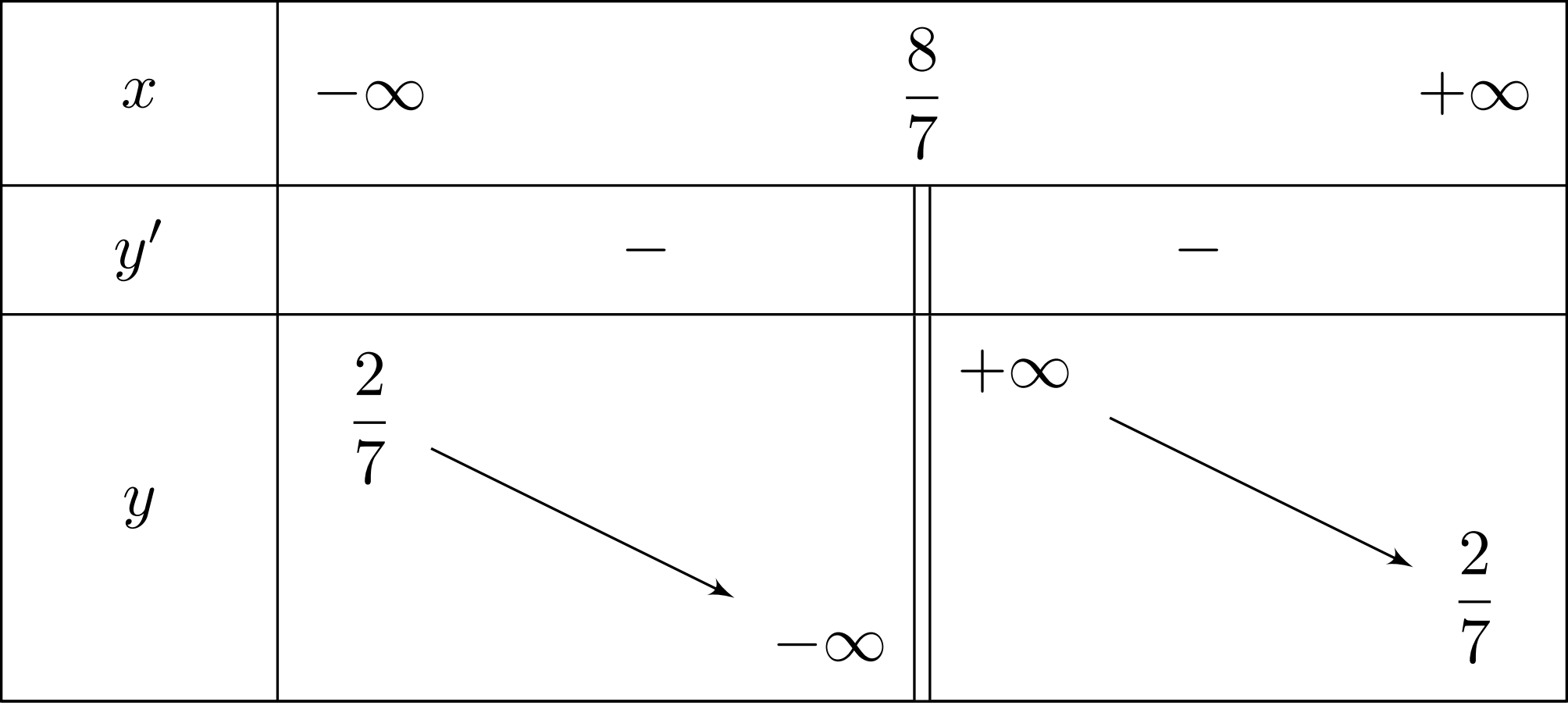
A. $y=\dfrac{x + 4}{7 x – 8}$.B. $y=\dfrac{2 x + 4}{7 x – 8}$.C. $y=\dfrac{2 x + 4}{7 x – 7}$.D. $y=\dfrac{- 2 x – 4}{7 x – 8}$.

Lời giải: Từ bảng biến thiên ta thấy
Hàm số nghịch biến.
Đồ thị hàm số có tiệm cận đứng là $x=\dfrac{8}{7}$ .
Đồ thị hàm số có tiệm cận ngang là $y=\dfrac{2}{7}$ .

Phân tích và Phương pháp giải

Dạng bài toán nhận dạng hàm số hữu tỉ bậc nhất $y = \dfrac{ax+b}{cx+d}$ dựa vào bảng biến thiên (BBT). Phương pháp giải là xác định các yếu tố: 1. Tiệm cận đứng (TCĐ): $x = x_0$ khi $cx_0 + d = 0$. 2. Tiệm cận ngang (TCN): $y = \dfrac{a}{c}$. 3. Tính đơn điệu (đồng biến/nghịch biến): Xét dấu của đạo hàm $y’ = \dfrac{ad-bc}{(cx+d)^2}$. Nếu $ad-bc > 0$ thì đồng biến, nếu $ad-bc < 0$ thì nghịch biến.

Bài toán tương tự

Từ bảng biến thiên, xác định hàm số $y=f(x)$ tương ứng. Các BBT được mô tả thông qua các tính chất của hàm số:\n\n\nCâu 1. Hàm số nào có bảng biến thiên mô tả đồ thị hàm số có tiệm cận đứng $x = -2$, tiệm cận ngang $y = 3$ và hàm số đồng biến trên từng khoảng xác định?\nA. $y = \dfrac{3x – 1}{x + 2}$.\nB. $y = \dfrac{3x + 7}{x + 2}$.\nC. $y = \dfrac{3x – 1}{x – 2}$.\nD. $y = \dfrac{-3x + 1}{x + 2}$.\nĐáp án đúng: A.\nGiải thích: TCĐ $x=-2$ (mẫu $x+2=0$). TCN $y=3$ ($a/c = 3/1 = 3$). Kiểm tra tính đơn điệu: $y’ = \dfrac{3(2) – (-1)(1)}{(x+2)^2} = \dfrac{7}{(x+2)^2} > 0$. Hàm số đồng biến. Vậy A là đáp án đúng.\n\n\nCâu 2. Hàm số nào có bảng biến thiên mô tả đồ thị hàm số có tiệm cận đứng $x = 0,5$, tiệm cận ngang $y = -2$ và hàm số nghịch biến trên từng khoảng xác định?\nA. $y = \dfrac{-4x + 5}{2x – 1}$.\nB. $y = \dfrac{-4x + 5}{2x + 1}$.\nC. $y = \dfrac{4x + 5}{2x – 1}$.\nD. $y = \dfrac{4x – 5}{2x – 1}$.\nĐáp án đúng: A.\nGiải thích: TCĐ $x = 1/2$ (mẫu $2x-1=0$). TCN $y = -2$ ($a/c = -4/2 = -2$). Xét tính nghịch biến của A: $y’ = \dfrac{(-4)(-1) – 5(2)}{(2x-1)^2} = \dfrac{4 – 10}{(2x-1)^2} = \dfrac{-6}{(2x-1)^2} < 0$. Hàm số nghịch biến. Vậy A là đáp án đúng.\n\n\nCâu 3. Hàm số nào có bảng biến thiên thể hiện TCĐ $x = 3$, TCN $y = 1$ và hàm số đồng biến trên từng khoảng xác định?\nA. $y = \dfrac{x + 1}{x + 3}$.\nB. $y = \dfrac{x + 1}{x – 3}$.\nC. $y = \dfrac{2x + 1}{x – 3}$.\nD. $y = \dfrac{x – 4}{x – 3}$.\nĐáp án đúng: D.\nGiải thích: TCĐ $x=3$ và TCN $y=1$. Loại A và C. Xét D: $y = \dfrac{x – 4}{x – 3}$. $y’ = \dfrac{1(-3) – (-4)(1)}{(x-3)^2} = \dfrac{1}{(x-3)^2} > 0$. Hàm số đồng biến. Vậy D là đáp án đúng.\n\n\nCâu 4. Hàm số nào sau đây có tiệm cận đứng $x = 5$, tiệm cận ngang $y = 4$ và nghịch biến trên từng khoảng xác định?\nA. $y = \dfrac{4x + 10}{x – 5}$.\nB. $y = \dfrac{4x – 10}{x + 5}$.\nC. $y = \dfrac{4x – 10}{x – 5}$.\nD. $y = \dfrac{x – 10}{4x – 5}$.\nĐáp án đúng: C.\nGiải thích: TCĐ $x=5$ và TCN $y=4$. Chỉ C thỏa mãn. Kiểm tra tính đơn điệu của C: $y’ = \dfrac{4(-5) – (-10)(1)}{(x-5)^2} = \dfrac{-10}{(x-5)^2} < 0$. Hàm số nghịch biến. Vậy C là đáp án đúng.\n\n\nCâu 5. Hàm số nào có bảng biến thiên mô tả đồ thị hàm số có TCĐ $x = -1/3$ và TCN $y = -1$, biết rằng hàm số này nghịch biến trên từng khoảng xác định?\nA. $y = \dfrac{-3x + 4}{3x + 1}$.\nB. $y = \dfrac{3x – 4}{3x + 1}$.\nC. $y = \dfrac{-x + 4}{3x + 1}$.\nD. $y = \dfrac{-3x – 4}{3x + 1}$.\nĐáp án đúng: A.\nGiải thích: TCĐ $x = -1/3$ và TCN $y = -1$. Loại B, C. Xét A: $y = \dfrac{-3x + 4}{3x + 1}$. $y’ = \dfrac{(-3)(1) – 4(3)}{(3x+1)^2} = \dfrac{-15}{(3x+1)^2} < 0$. Hàm số nghịch biến. Vậy A là đáp án đúng.