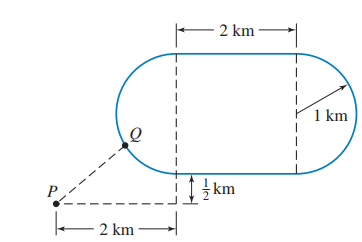
Hình cho thấy một mặt bằng đường đua bao gồm hai cạnh của một hình chữ nhật và hai nửa đường tròn. Ngoài ra còn cho vị trí ${P}$ của một khán giả đang xem đua từ trên nóc xe của mình. Hãy tìm điểm ${Q}$ trên đường đua sao cho khoảng cách từ ${P}$ đến đường đua là nhỏ nhất. Tính khoảng cách giữa hai điểm đó.
Lời giải
Rõ ràng điểm cần tìm phải nằm trên cung nửa đường tròn ở góc dưới bên trái của đường đua. Chúng ta thiết lập hệ tọa độ như ở Hình 8, với tâm của hình tròn ở gốc tọa độ và bán kính bằng 1.
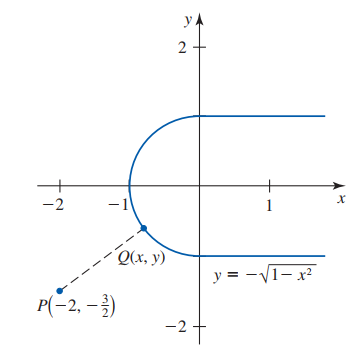
Phương trình của đường tròn là ${{x}^{2}}+{{y}^{2}}=1$
Do chỉ xét nửa dưới bên trái, tức ${x \leq 0}$ và ${y \leq 0}$, ta giải được $y=-\sqrt{1-{{x}^{2}}},\quad -1\le x\le 0$(1)
Gọi ${D}$ là khoảng cách giữa ${P\left(-2,-\frac{3}{2}\right)}$ và một điểm ${Q(x, y)}$ trên cung.
Áp dụng công thức khoảng cách, $D=\sqrt{{{(x-(-2))}^{2}}+{{\left( y-\left( -\frac{3}{2} \right) \right)}^{2}}}=\sqrt{{{(x+2)}^{2}}+{{\left( y+\frac{3}{2} \right)}^{2}}}$
Do đó ${{D}^{2}}={{(x+2)}^{2}}+{{\left( y+\frac{3}{2} \right)}^{2}}={{x}^{2}}+4x+4+{{y}^{2}}+3y+\frac{9}{4}$(2)
Vì ${D}$ nhỏ nhất khi và chỉ khi ${D^2}$ nhỏ nhất, ta sẽ đi tìm cực tiểu của ${D^2}$.
Thay ${y}$ từ (1) vào (2): ${{D}^{2}}={{x}^{2}}+4x+4+\left( 1-{{x}^{2}} \right)-3\sqrt{1-{{x}^{2}}}+\frac{9}{4}=4x-3\sqrt{1-{{x}^{2}}}+\frac{29}{4}$
Vậy bài toán tương đương với việc tìm ${x \in[-1,0]}$ để hàm $f(x)=4x-3\sqrt{1-{{x}^{2}}}+\frac{29}{4}$
nhận giá trị nhỏ nhất.
– Tính đạo hàm:
${{f}^{\prime }}(x)={{\left[ 4x-3{{\left( 1-{{x}^{2}} \right)}^{1/2}}+\frac{29}{4} \right]}^{\prime }}=4-3\cdot \frac{1}{2}{{\left( 1-{{x}^{2}} \right)}^{-1/2}}\cdot (-2x)=4+\frac{3x}{\sqrt{1-{{x}^{2}}}}$
– Giải ${f^{\prime}(x)=0}$: $4+\frac{3x}{\sqrt{1-{{x}^{2}}}}=0\Leftrightarrow 3x=-4\sqrt{1-{{x}^{2}}}\Leftrightarrow 9{{x}^{2}}=16\left( 1-{{x}^{2}} \right)\Leftrightarrow 25{{x}^{2}}=16$
cho ${x= \pm \frac{4}{5}}$. Trong đó chỉ ${x=-\frac{4}{5}}$ nằm trong ${[-1,0]}$.
So sánh giá trị:
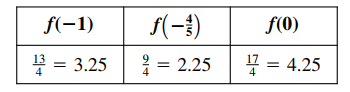
Như vậy ${f}$ nhỏ nhất bằng 2.25 tại ${x=-\frac{4}{5}}$. Từ (7) ta có $y=-\sqrt{1-{{\left( -\frac{4}{5} \right)}^{2}}}=-\frac{3}{5}$
Do đó điểm cần tìm là $Q\left( -\frac{4}{5},-\frac{3}{5} \right).$
Khoảng cách từ ${P}$ đến ${Q}$ là $D=\sqrt{f\left( -\frac{4}{5} \right)}=\sqrt{\frac{9}{4}}=\frac{3}{2}$ hay ${1,5({~km})}$.
