Hiệu quả nhiên liệu E, tính bằng số kilômét đi được trên mỗi lít xăng $\left( km/l \right)$, của một mẫu xe ôtô được mô hình hóa theo tốc độ $v\,\,\left( km/h \right)$ bằng công thức sau: $E\left( v \right)=-0,000025{{v}^{3}}+0,003{{v}^{2}}+13,5$

Hiệu quả nhiên liệu E, tính bằng số kilômét đi được trên mỗi lít xăng $\left( km/l \right)$, của một mẫu xe ôtô được mô hình hóa theo tốc độ $v\,\,\left( km/h \right)$ bằng công thức sau: $E\left( v \right)=-0,000025{{v}^{3}}+0,003{{v}^{2}}+13,5$. Mô hình này được áp dụng cho các tốc độ $v$ từ $20\,km/h$ đến $120\,km/h$ $\left( 20\le v\le 120 \right)$. Tìm giá trị nhiên liệu hiệu quả nhất (tức là đi được nhiều km nhất trên mỗi lít xăng, làm tròn đến hàng phần mười)?

Lời giải

Đáp án: $19,9$.

Ta có: $E’\left( v \right)=-0,000075{{v}^{2}}+0,006v$

$E’\left( v \right)=0\Leftrightarrow \left[ \begin{matrix}

v=0 \\

v=80 \\

\end{matrix} \right.$.

Bảng biến thiên của hàm số $E\left( v \right)$ với $20\le v\le 120$ như sau:

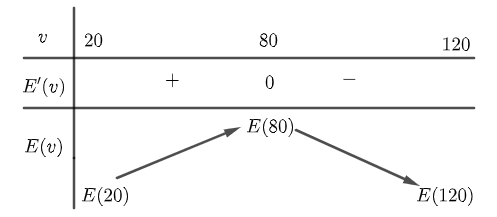
Do đó giá trị nhiên liệu hiệu quả nhất là $E\left( 80 \right)=19,9$.