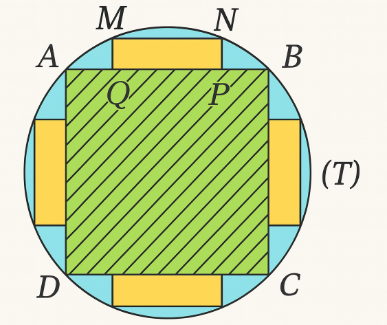
Bác Bình sử dụng một khúc gỗ hình trụ có đường kính bằng ${32}$ cm để làm một chiếc xà nhà. Để đảm bảo tính thẩm mĩ thì bác Bình dự định sẽ cho thợ xẻ khúc gỗ thành một chiếc xà có tiết diện ngang (là miền gạch sọc như hình vẽ bên) bao gồm một hình vuông ${ABCD}$ và $4$miếng phụ là 4 hình chữ nhật bằng nhau. Bốn điểm ${A, B, C, D}$ nằm trên đường tròn ${(T)}$; miếng phụ ${MNPQ}$ có hai đỉnh ${M, N}$ nằm trên đường tròn ${(T)}$ và hai đỉnh ${P, Q}$ nằm trên cạnh ${AB}$. Mặt khác, diện tích của tiết diện ngang càng lớn thì chiếc xà chịu lực càng tốt. Hỏi bác Bình có thể tạo ra một tiết diện ngang có diện tích lớn nhất bằng bao nhiêu centimet vuông (làm tròn kết quả đến hàng đơn vị)?
Lời giải
Đáp án: 684.
Đặt $MQ=x$, $MN=y$ (Đk: $0<x,y<8\sqrt{2}$)
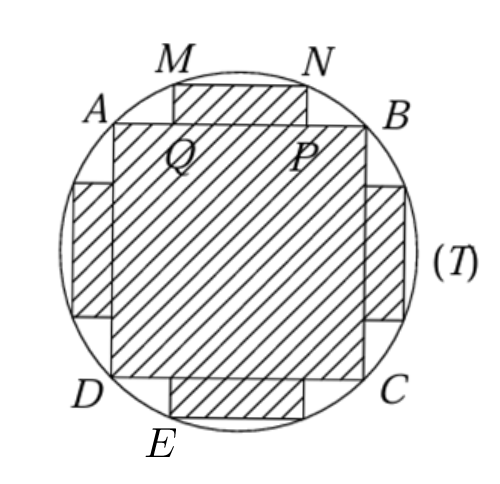
Có $AC=32=NE$ và $AD=\frac{32}{\sqrt{2}}=16\sqrt{2}$, $ME=16\sqrt{2}+2x$.
Xét tam giác $MNE$: $N{{E}^{2}}=M{{E}^{2}}+M{{N}^{2}}$
$\Rightarrow y=\sqrt{512-64\sqrt{2}x-4{{x}^{2}}}$.
Do đó ${{S}_{MNPQ}}=x\cdot y=x\sqrt{512-64\sqrt{2}x-4{{x}^{2}}}$
$=\sqrt{512{{x}^{2}}-64\sqrt{2}{{x}^{3}}-4{{x}^{4}}}$.
Xét hàm số $f\left( x \right)=512{{x}^{2}}-64\sqrt{2}{{x}^{3}}-4{{x}^{4}}$, $x\in \left( 0;8\sqrt{2} \right)$.
Ta có ${f}’\left( x \right)=0\Leftrightarrow 1024x-192\sqrt{2}{{x}^{2}}-16{{x}^{3}}=0$
Sử dụng casio, ta tìm được ${{x}_{0}}\approx 3,17$.
Khi đó: ${{\left( {{S}_{MNPQ}} \right)}_{\max }}=\sqrt{f\left( {{x}_{0}} \right)}\approx 43,1$
Vậy ${{S}_{\max }}={{S}_{ABCD}}+4\sqrt{f\left( {{x}_{0}} \right)}={{\left( 16\sqrt{2} \right)}^{2}}+4.43,1\approx 684$
